
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Рунге-Кутта
|
|
Наиболее распространеннымв практике интегрирования обыкновенных дифференциальных уравнения является метод Рунге-Кутта. При его использовании решение уравнений представляется в виде итерационных формул Рунге-Кутта.
Пусть дано уравнение
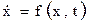 ,
,
удовлетворяющее начальному условию 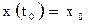 .
.
Выберем достаточно малый шаг и построим систему равноотстоящих точек:
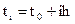 ,
, 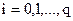 .
.
Рассмотрим метод Рунге-Кутта четвертого порядка:
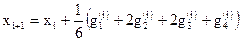 ,
,
где
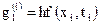 ,
,
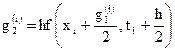 ,
,
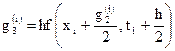 ,
,
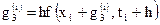 .
.
Достоинством метода Рунге-Кутта является то, что при его использовании нет необходимости вычислять производные выше первого порядка, аосновные недостатки – громоздкость и значительный объем вычислений на каждом шаге.
Алгоритм численного интегрирования
дифференциальных уравнений методом Рунге-Кутта
Вданной задаче исходная система уравнений имеет вид:
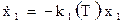 ,
, 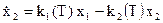
с начальными условиями 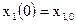 ,
, 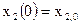 .
.
Сопряженная система уравнений:
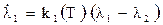 ,
, 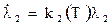
с граничными условиями 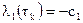 ,
, 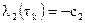 .
.
Зададим начальные условия 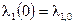 ,
, 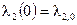 .
.
1. Для интегрирования уравнений в интервале времени от t до 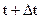 разобьем интервал на Р частей с шагом
разобьем интервал на Р частей с шагом 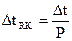 .
.
2. Пусть 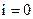 . Определяем значение
. Определяем значение 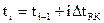 .
.
3. Для уравнений исходной и сопряженной систем определяем величины: 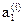 ,
,  ,
, 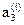 ,
, 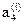 ;
; 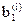 ,
, 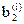 ,
, 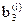 ,
, 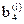 ;
; 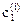 ,
, 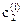 ,
, 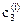 ,
, 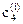 ;
; 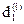 ,
, 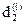 ,
, 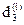 ,
, 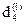 .
.
Для уравнения 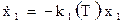 :
:
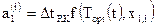 ,
,
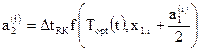 ,
,
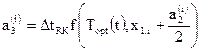 ,
,
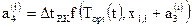 .
.
Для уравнения 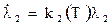 :
:
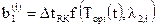 ,
,
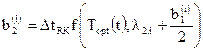 ,
,
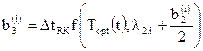 ,
,
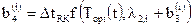 .
.
Для уравнения 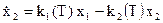 :
:
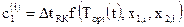 ,
,
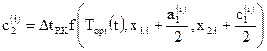 ,
,
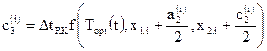 ,
,
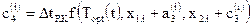 .
.
Для уравнения 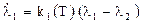 :
:
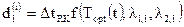 ,
,
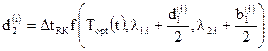 ,
,
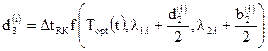 ,
,
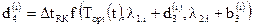 .
.
4. Далее вычисляем:
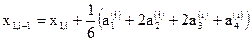 ,
,
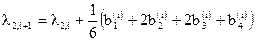 ,
,
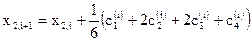 ,
,
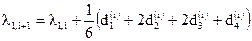 .
.
5. Процедуру вычисления значений 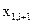 ,
, 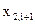 ,
, 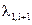 ,
, 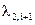 повторяем при последующих значениях
повторяем при последующих значениях 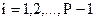 .
.