Порядок выполнения работы. 1. Изучить принцип максимума.

1. Изучить принцип максимума.

2. Получить задание и исходные данные у преподавателя согласно табл. 3.1.

3. Разработать алгоритм решения задачи оптимизации реактора идеального вытеснения и составить блок-схему.

4. Написать программу решения задачи на ЭВМ.

5. Исследовать влияние величины рабочего шага поиска начальных условий для интегрирования сопряженных систем уравнений на погрешность расчета.

6. Проанализировать влияние величины шага интегрирования в методе Рунге-Кутта на оптимальные фазовые траектории концентраций и температурный профиль по длине реактора.

7. Подготовить ответы на контрольные вопросы.

Работа в лаборатории

1. Ввод и отладка программы на ЭВМ.

2. Обработка и анализ результатов расчета.

3. Построение оптимального температурного профиля 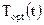; оптимальных фазовых траекторий 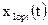, 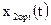; графика зависимости максимальных значений функции Гамильтона от времени 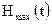; графиков зависимостей , .

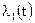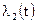Содержание отчета о работе

1. Постановка задачи. Задание.

2. Алгоритм решения задачи и блок-схема алгоритма.

3. Листинг программы решения задачи.

4. Результаты расчета.

5. Графическое представление функций: , , , , , .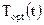

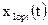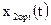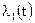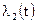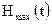6. Основные выводы и заключения.

Контрольные вопросы

1. Привести формулировку принципа максимума.

2. Расскажите о свойствах функции Н.

3. В чем состоит простота и трудность решении задачи с использованием принципа максимума?

4. Для решения какихзадач следует применять принцип максимума?

5. Сформулируйте задачу со свободным правым концом.

6. Для каких систем принцип максимума является необходимым и достаточным условием оптимальности.

7. Расскажите алгоритм численного решения задачи на основе принципа максимума.

8. Как записываются условия максимума функции Гамильтона в задаче без ограничений?

Таблица 3.1

Варианты заданий к задаче оптимизации

реактора идеального вытеснения

№
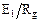
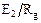
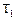
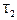
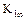
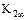
					3.5	0.5
						0.3
						0.9
						0.6
						0.8
					3.6	0.6
						0.6
						0.9
					3.5	0.5
					3.8	0.55
						0.7
						0.3
					3.8	0.55
					3.5	0.5
						0.6
						0.65
						0.7
						0.65
						0.6