
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Операции над множествами. U – универсум- множество элементов, обладающих каким-то одним общим свойством.
|
|
 U – универсум- множество элементов, обладающих каким-то одним общим свойством.
U – универсум- множество элементов, обладающих каким-то одним общим свойством.
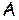 = < A, {
= < A, { 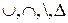 }>
}>
 |
сигнатура
Множества А, В, С, … 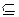 U
U
1. Объединение (теоретико-множественная сумма).
2. Пересечение (произведение множеств).
3. Разность.
4. Симметрическая разность.
Df1. Объединением двух множеств А и В называется третье множество (обозначается 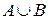 ), которому принадлежат элементы из множества А или же элементы из множества В:
), которому принадлежат элементы из множества А или же элементы из множества В: 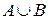 = {x | x
= {x | x 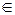 A или x
A или x 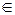 B}
B}
Пример:
А = {1, 2, 3} 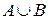 = {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
B = {3, 4, 5}
В силу записи множеств одинаковые элементы можно опустить.
Удобно операции демонстрировать или изображать графически с помощью диаграмм или кругов Эйлера-Венна, при этом универсум обозначается прямоугольником (иногда обозначают универсум 1).
|


Объединение 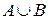 Пересечение
Пересечение 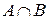
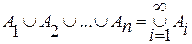
Разрешается следующая запись: если n – счетное число (когда n 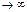 ), то можно записать
), то можно записать
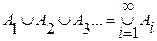 .
.
Когда в качестве элементов записываются сами множества
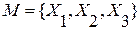 , где Х1, Х2, Х3 – множества
, где Х1, Х2, Х3 – множества
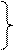
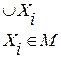
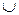 - фактически это знак суммы
- фактически это знак суммы
Df2. Пересечением двух множеств А и В называется такое третье множества (обозначается 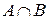 ), которому принадлежат элементы из множества А и элементы из множества В:
), которому принадлежат элементы из множества А и элементы из множества В: 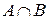 = {x |
= {x | 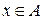 и
и 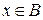 }
}
Пример:
А = {1, 2, 3} 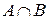 ={3}
={3}
B = {3, 4, 5}
Допускается запись такого вида
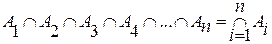
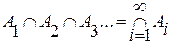
М = {X1, X2, X3}, где X1, X2, X3 – множества
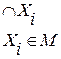
1) 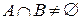 , А и В не пусто, т.е. они пересекаются.
, А и В не пусто, т.е. они пересекаются.
2) Если множества А и В не имеют общих элементов, то говорят 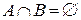 , они не пересекаются:
, они не пересекаются:
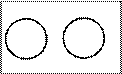 U
U
А В
Df3. Разностью двух множеств А и В называется такое третье множество (обозначается А\В), которому принадлежат элементы множества А и не принадлежат элементы множества В: А\В = {x | 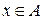 и
и 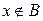 }
}
Пример:
А = {1, 2, 3} A\B = {1, 2}
B = {3, 4, 5} B\A = {4, 5}
Df4. Симметрической разностью двух множеств А и В называется такое третье множество (обозначается 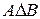 ), которому принадлежат только элементы множества А и элементы множества В:
), которому принадлежат только элементы множества А и элементы множества В:
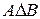 = {x |
= {x | 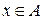 и
и 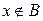 ,
, 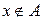 и
и 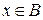 }.
}.
Допускается запись 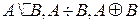
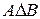 = (A\B)
= (A\B) 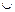 (B\A) для симметрической разности.
(B\A) для симметрической разности.
| |||
| |||


Df5. Дополнение множества Х до U: U\X = 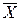 , где U – универсальное множество
, где U – универсальное множество
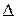 B = {1, 2, 4, 5}
B = {3, 4, 5}
B = {1, 2, 4, 5}
B = {3, 4, 5}