
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кортеж (вектор).
|
|
Кортежи принято обозначать 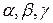 …
…
Если раньше мы считали, что {a, b} = {b, a}, то в кортеже такие перестановки не возможны.
 =< a, b> - кортеж.
=< a, b> - кортеж.
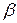 =< a1, a2, …, an>, где a1…an – компоненты (элементы) кортежа.
=< a1, a2, …, an>, где a1…an – компоненты (элементы) кортежа.
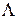 = < > – пустой кортеж.
= < > – пустой кортеж.
 =< a> – кортеж из одной компоненты.
=< a> – кортеж из одной компоненты.
 =< a, b> – кортеж из 2-х компонент.
=< a, b> – кортеж из 2-х компонент.
 ={{a}, {a, b}} – эта запись означает, что кортеж
={{a}, {a, b}} – эта запись означает, что кортеж  состоит из двух элементов, в расположении двух элементов первым стоит а.
состоит из двух элементов, в расположении двух элементов первым стоит а.
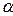 =< a1, а2, …, аn> – кортеж из n компанент.
=< a1, а2, …, аn> – кортеж из n компанент.
Если указана природа элементов кортежа 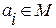 и строится кортеж
и строится кортеж  =< a1, а2, …, аn>, то говорят, что имеем кортеж
=< a1, а2, …, аn>, то говорят, что имеем кортеж 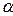 над множеством М.
над множеством М.
Свойства кортежей:
1) < a, b> 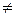 < b, а>;
< b, а>;
2) два кортежа 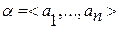 и
и 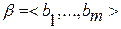 равны между собой тогда и только тогда, когда равны их компоненты, стоящие на одинаковых местах и количество компонент совпадает:
равны между собой тогда и только тогда, когда равны их компоненты, стоящие на одинаковых местах и количество компонент совпадает: 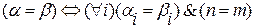
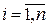
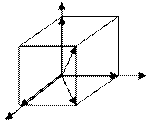
3) Проектирование кортежей

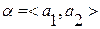
Операция разложения вектора по осям называется
проектированием кортежа (а1 и а2 – проекции)
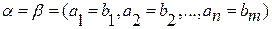 (n=m)
(n=m)

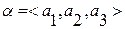
пр1  = а1
= а1
пр2  = а2
= а2
пр3  = а3
= а3
аi = прi  = < a1, …, ai, …an>
= < a1, …, ai, …an>
прi1, i2…ik  = < a1, a2, …ai1, ai2, …aik, …an> = < ai1, ai2, …aik>
= < a1, a2, …ai1, ai2, …aik, …an> = < ai1, ai2, …aik>
Проекция кортежа на несколько осей есть кортеж. Если говорят, что элементы кортежа  берутся из конкретного множества М, то можно говорить о проекции кортежа
берутся из конкретного множества М, то можно говорить о проекции кортежа  над множеством М.
над множеством М.
Свойства кортежей:
1. рефлексивность:  =
=  .
.
2. симметричность: если кортеж  равен кортежу
равен кортежу 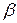 , то очевидно, что
, то очевидно, что 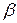 =
=  .
.
3. транзитивность.
Если кортеж  равен кортежу
равен кортежу 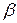 , а он в свою очередь равен кортежу
, а он в свою очередь равен кортежу 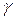 , то кортеж
, то кортеж  равен кортежу
равен кортежу 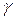 : [
: [  =
= 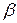 ;
; 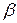 =
= 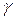 ] =>
] =>  =
= 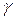 .
.