
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематическое исследование механизма
|
|
В задачу кинематического анализа входит определение законов движения звеньев механизма, вне зависимости от сил действующих на эти звенья.
Построение планов положений
По исходным данным вычерчивается схема механизма в произвольно выбранном масштабе. Масштабный коэффициент указывает количество единиц изображаемой величины в 1 мм чертежа. При построении планов механизма желательно масштабный коэффициент m l [м/мм] выбирать из следующего ряда: 0, 001; 0, 002; 0, 0025; 0, 004; 0, 05; 0, 08; 0, 1 и т. д.
Пусть заданный размер звена l ОА= 0, 08 м (l ОА=Нв/2) будет изображен на чертеже отрезком ОА = 40 мм. Тогда масштабный коэффициент m l = l ОА/ОА = 0, 08/40 = 0, 002 м/мм.
Определяем величину отрезка, изображающего длину звена АВ на чертеже
l AB = l OA · l = 0, 08·4, 45 = 0, 356 м
AB = l AB / m l = 0, 356 / 0, 002 = 178мм
Построение начинаем с изображения неподвижных элементов. Наносим на чертеже точку О (ось вращения звена 1) и проводим траекторию y-y точки В ползуна 3. Далее радиусом ОА проводим окружность, представляющую собой траекторию точки А.
На этой окружности на одинаковом расстоянии друг от друга (j =30°) наносим положение т. А (1, 2, 3...). Соединив их отрезками прямых с точкой О, получим соответствующие положения кривошипа. За начало отсчета принимаем точку А0, соответствующую крайнему верхнему положению ползуна (кривошип ОА и шатун АВ вытянулись в одну прямую).
Так как данный механизм относится ко второму классу, то положения звеньев гр. Ассура определим методом засечек.
Положение точки В (группа 2, 3) определим засечкой, сделанной из т. А радиусом АВ на траектории точки В. Соединив точку В с точкой А прямым отрезком, найдем положения звеньев 2 и 3.
Таким образом, строятся все 12 положений механизма. При этом заданное положение механизма (координата j1 для силового анализа) выделяется основными линиями, а остальные положения вычерчиваются тонкими линиями.
Построение планов скоростей
Построение планов скоростей и ускорений основано на графическом решении векторных уравнений.
Определение линейных скоростей и ускорений точек механизма начинается с механизма первого класса, а затем в порядке присоединения групп Ассура.
1(1, 4)=> 2(2, 3).
Рассмотрим построение плана скоростей для заданного, первого
положения механизма. Модуль скорости точки А кривошипа, совершающего вращательное движение относительно стойки, определим
VА = ω 1· lОА= 471· 0, 08 =37, 68 м/с,
где ω 1=π · n/ 30 = 3, 14 • 4500/30 = 471 с-1.
Вектор скорости VA направлен перпендикулярно радиусу кривошипа в сторону его вращения.
Выбираем масштабный коэффициент mV=0, 5 мс-1/мм, тогда отрезок p a изображающий скорость точки А на чертеже определится
pa = VA / mV= 37, 68 / 0, 5 = 75, 36 мм.
Из произвольной точки р — полюса плана скоростей откладываем в указанном направлении отрезок ра.
Для определения скоростей точек в структурной группе, составляют два векторных уравнения, связывающих искомую скорость точки с известными скоростями точек.
В группе Ассура (2, 3) определяем скорость центра шарнира В, который соединяет звенья 2 и 3. Рассматривая движение точки В по отношению к точке А, а затем по отношению к точке В4, запишем 2 векторных уравнения:
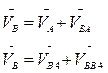
В этой системе векторных уравнений известны по модулю и направлению векторы скоростей точек А и В4. VB4=0, т. к. точка В4 принадлежит стойке. Векторы относительных скоростей известны
по линии действия. Скорость VBA направлена по перпендикуляру к звену АВ, а скорость VBB4 направлена параллельно направляющей y-y.
Решаем векторные уравнения графически. Согласно первому уравнению, через точку а проводим прямую перпендикулярно звену АВ, а согласно второму, через точку р (так как VB4 = 0 и точка В4 лежит в полюсе) проводим прямую параллельно y-y. На пересечении этих перпендикуляров отмечаем точку в, которая является концом вектора рв, изображающего абсолютную скорость точки B. Направление скорости определяем в соответствии с уравнением 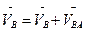
Скорость точки S2 находим из теоремы подобия. Исходя из пропорции 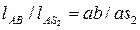 отрезок
отрезок 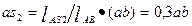 .
.
Соединим точку s2 с полюсом р получаем вектор ps2 — скорость точки s2.
Пользуясь масштабным коэффициентом μ v, определяем значение скоростей
VB= (р в)· μ у = 45, 43 • 0, 5 = 22, 7 м/с
VS2= (ps2)· μ у = 61 · 0, 5 = 30, 5 м/с
VBA= (aв)· μ у = 66 · 0, 5= 33 м/с
Находим угловую скорость ω 2 звена 2
w2 = VBA / l AB = 33/0, 356 = 92, 7 c-1
Направление ω 2 определим, перенося вектор ав скорости VBA в точку В и рассматривая движение точки В относительно точки А в направлении скорости VBA. Все определенные скорости заносим в таблицу.
| Таблица 2.2 | Значения линейных и угловых скоростей | Положение механизма | 45, 43 | 22, 7 | 30, 5 | 92, 7 | ||||
| 19, 5 | 73, 32 | 36, 7 | 36, 5 | 54, 8 | ||||||
| 19, 5 | 58, 29 | 29, 1 | 34, 5 | 54, 8 | ||||||
| 30, 55 | 15, 3 | 92.7 | ||||||||
| 26, 5 | 106, 7 | |||||||||
| 30, 57 | 15, 3 | 92, 7 | ||||||||
| 19, 5 | 58, 3 | 29, 1 | 34, 5 | 54, 8 | ||||||
| 19, 5 | 73, 32 | 36, 7 | 36, 5 | 54, 8 | ||||||
| 45, 43 | 22, 7 | 30, 5 | 92, 7 | |||||||
| 26, 5 | 106, 7 | |||||||||
| ab | VBA | pb | VB | ps2 | VS2 | ω 2 |
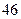
Построение плана ускорений
Для механизма первого класса определяем ускорение точки А, совершающей вращательное движение по окружности радиуса l ОА Условно принимаем, что e1= 0, тогда
аА= аnA=ω 12· lОА= 4712· 0, 08 = 17747, 28 м/с2
Вектор π а ускорения аA=аnA направлен по звену ОА от точки А к точке О. Выбираем масштабный коэффициент μ а = 300 мс-2/мм, тогда отрезок π а изображающий ускорение точки А на чертеже определится
π а = аА / μ а = 17748, 28/300 = 59 мм.
Отложив из произвольно взятой точки π (полюса) вектор π а параллельно ОА получим план ускорений для механизма первого класса.
В группе Ассура (2, 3) определяем ускорение точки В.
Рассматривая движение точки В сначала по отношению к точке А (относительное движение звена 2 — вращательное вокруг точки А), а затем по отношению к точке В4.
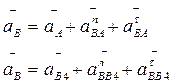 |
Ускорение aA и аВ4 точек А и В4 известны (a В4=0).
Величина нормального ускорения вычисляется по формуле:
anBA = w22· lAB = 92, 72 · 0, 356 = 3081, 28 м/с2
Вектор a nВА направлен параллельно звену АВ от точки В к точке А.
Направление векторов тангенциального ускорения a τ ВА точки В относительно точки А и тангенциального ускорения а τ ВВ4 точки В относительно точки В4 известны — а τ ВА ┴ AB, аτ ВВ4 ||y-y. Решаем уравнение графически. В соответствии с первым уравнением из точки а плана ускорений откладываем отрезок an 2, изображающий ускорение а nВА,
an2 = апВА/μ а = 3081, 28/300 = 10, 27 мм
Отрезок аn2 проводим параллельно звену АВ в направлении от точки В звена к точке А. Через точку n2 проводим перпендикуляр к звену АВ — направление а τ ВА.
В соответствии со вторым уравнением через точку π (так как a B4 = 0 и a kBB4 =0) проводим параллельно y-y направление вектора а τ ВВ4. Эти направления пересекутся в точке в.
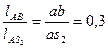 В соответствии с теоремой подобия точка S2 на плане ускорений находится из пропорции
В соответствии с теоремой подобия точка S2 на плане ускорений находится из пропорции
as2= 0, 3 ав
Соединяя точку s2 с полюсом π получим вектор ускорения a S2.
План ускорений построен. Из плана определим величины ускорений:
a В= (π в)· μ a =57, 63· 300 =17289 м/с2
a S2= (π s2)· μ a =57, 07· 300=17121 м/с2
a τ ВА= (n2 в) · μ a =28, 52 · 300=8556 м/с2
Величину углового ускорения e2, звена 2 определим следующим образом:
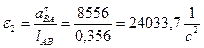
Для определения направления e2 переносим вектор n2 в ускорения a tBА в точку В звена 2 и смотрим движение точки В относительно точки А.
2.3. Динамический синтез и анализ движения машины
При динамических исследованиях машин и механизмов, как правило, с целью упрощения производится идеализация реальной системы, которая сводится к построению динамической модели, позволяющей абстрагироваться от конкретной конструкции, но при этом сохранить неизменными основные динамические свойства системы.
В первом приближении часто ограничиваются исследованием систем с одной степенью свободы, считая условно, что все звенья механизмов, входящих в состав машины, являются абсолютно твердыми телами.
Для систем с одной степенью свободы в качестве динамической модели принимается вращающееся статически уравновешенное твердое тело или точечные поступательно
движущиеся или вращающиеся массы. Причем чаще всего модель размещается на входном звене основного механизма машины, так как именно закон движения входного звена необходимо определять в первую очередь при динамическом исследовании.
При построении динамической модели необходимо соблюдать следующие условия динамической эквивалентности.
1. Силы или моменты сил, приложенные к динамической модели, производят на возможном перемещении работу, равную (за равный промежуток времени) сумме работ всех сил и моментов, действующих на механизм на их возможных перемещениях. Мгновенная мощность, развиваемая силами или моментами на динамической модели, равна сумме мощностей, развиваемых всеми силами и моментами, действующими на механизм.
2. Динамическая модель должна обладать условной массой или моментом инерции массы, которые при скорости модели способны развить кинетическую энергию, равную сумме кинетических энергий, развиваемых всеми звеньями механизма, т. е. равную кинетической энергии механизма.
Звено, на котором размещается модель, принято называть звеном приведения; его массу или момент инерции — приведенной массой или приведенным моментом инерции; действующие на него силы и моменты сил — приведенными силами или приведенными моментами сил (обобщенными силами).
Кинетическая энергия механизма с одной степенью свободы (динамическая модель — твердое тело)
Т=1/2·Iпр.·w2,
где Т — кинетическая энергия, [Дж];
Iпр. — приведенный момент инерции, [кг·м2];
w — угловая скорость звена проведения, [рад/с].
Отсюда
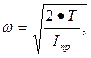
Таким образом, угловая скорость звена приведения зависит от изменения кинетической энергии и приведенного момента инерции всех звеньев механизма.
Каждый цикл установившегося движения характеризуется равенством работ сил движущих и сил сопротивления, т. е.
|Aдв.|ц. = |Асопр.|ц.
В пределах цикла (2p) это равенство, как правило, нарушается, что приводит к периодическому изменению угловой скорости звена приведения от wmin до wmах. Эти колебания оцениваются коэффициентом неравномерности d.
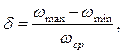 |
где wср. — средняя угловая скорость, которая соответствует номинальному (заданному) значению.
Для ограничения колебаний скорости w и, следовательно,
величины d искусственно увеличивают Iпр, устанавливая дополнительную массу — маховое колесо (маховик).
Определение Iм, обеспечивающего заданный коэффициент неравномерности движения механизма, может быть выполнено различными методами. Сравнительная простота, наглядность, возможность оценки изменения угловой скорости звена приведения отличает метод профессора Н. И. Мерцалова.
В общем случае кинетическая энергия механизма может быть выражена следующим образом:
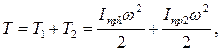 |
где T1 — кинетическая энергия звена приведения, маховика и звеньев, связанных со звеном приведения постоянством передаточного отношения (первая группа звеньев);
Т2 — кинетическая энергия звеньев приведенный момент инерции которых переменен (вторая группа звеньев);
Iпр.1 — приведенный момент инерции первой группы звеньев (Iпр.1=const);
Iп 2 — приведенный момент инерции второй группы звеньев.
Т1=Т – Т 2
В связи с неравномерностью вращения звена приведения величина кинетической энергии первой группы звеньев колеблется от Т1 mах до Т1 min.
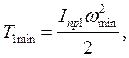
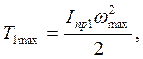
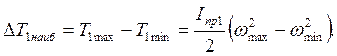
Если принять, что 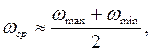
то 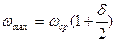
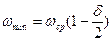 .
.
Отсюда w2max» w2ср (1+d), а w2min» w2ср (1-d).
Следовательно DT1наиб = Iпр1 w2ср · d
Решая относительно Iпр1 получим:
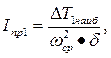
Значение DТ1наиб. определяется амплитудой графика DТ1(j), который по Мерцалову строится из следующих соображений.
Кинетическая энергия всего механизма выражается равенством
Т=Тнач.+DТ=Т1 + Т2.
Отсюда Т1 = Тнач. + DT — Т2,
Тнач — кинетическая энергия всего механизма в начале цикла, ее значение постоянно и не влияет на характер графика DТ1(j), и его амплитуду;
DT — изменение кинетической энергии всего механизма;
Известно, что изменение кинетической энергии механизма происходит за счет работы всех сил и моментов, приложенных к механизму, поэтому запишем
 |
где Мпр.д. — приведенный момент движущих сил, Н • м;
Мпр.с. — приведенный момент сил сопротивления, Н • м.
После алгебраического суммирования графиков работ Ад(j) и Ас(j), которые строятся методом графического интегрирования зависимостей Мпр.д. (dj) или Мпр.с. (dj), строится график DT (j).
Полагая wср.=const (в связи с тем, что Iпр.2 изменяется намного интенсивнее, чем w), найдем
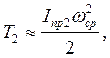 |
Таким образом, график Т2(j) тождественен графику Iпр2(j) и отличается от него только величиной вычислительного масштаба.
Определив значения T1 путем вычитания из кривой DT кривой Т2, и построив график DT1(j), найдем максимальное изменение его амплитуды, то есть DТ1mах .