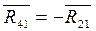Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение диаграммы работ
|
|
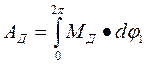
Диаграмму работ сил движущих строим методом графического интегрирования диаграммы Мпр.д=f(j1).
Метод графического интегрирования заключается в следующем. Плавную кривую диаграммы Мпр.д=f(j1) заменяем ступенчатой из условия равенства площадей, на элементарных участках, ограниченных обеими диаграммами. Для этого необходимо, чтобы на каждом участке площади заштрихованных площадок, расположенных по обе стороны кривой, были равны. Это достаточно точно устанавливается на глаз.
Выбираем на оси абсцисс слева от начала координат на произвольном расстоянии Н точку Р. Соединим эту точку с точками 1', 2', 3' и т. д. ступенчатой диаграммы лежащими на оси ординат, получим лучи Р-1'; Р-2'; Р-3' и т. д.
Под диаграммой Мпр.д=f(j1) проводим оси координат диаграммы
A=f(j1) и разбиваем ось j на участки, равные соответствующим участкам диаграммы Мпр.д=f(j1). Далее на участке 0-1 проводим из начала координат отрезок 0-1", параллельный лучу Р-1"; из полученной точки 1" на участке 1-2 проводим отрезок 1" -2" параллельный Р-2"; из точки 2" проводим отрезок 2" -3", параллельный лучу Р-3" и т. д. Полученная ломаная линия представляет собой диаграмму AД =f (j1). Заменяем ломаную линию плавной кривой.
Масштабный коэффициент определяется по формуле
mА = mМ·mj ·Н = 5, 5·0, 04·47 = 10, 34 (Дж/мм)
Для построения диаграммы работ сил сопротивления достаточно соединить прямой точки 0 и 12 диаграммы Aд =f (j1).
2.3.3. Диаграмма приращения кинетической энергии машины с маховиком DТ=f (j1) (суммарная работа)
Так как сумма работ всех сил действующих на машину, равна изменению кинетической энергии DТ(SА=DТ=АД - АС), то график DТ=f (j1) получаем в результате алгебраического сложения положительных ординат диаграммы AД =f (j1) и отрицательных ординат диаграммы AС =f (j1).
Практически результат получают путем графической разности ординат указанных графиков. При этом учитываем, что если ордината АД > Ас, то SА и DT положительны, если
ордината АД < Ас, то SА и DT отрицательны.
Диаграмму приращения кинетической энергии получаем в масштабе:
mТ = mА (Дж/мм).
2.3.4. Определение кинетической энергии звеньев, имеющих переменный приведенный момент инерции (Т2)
Кинетическая энергия звеньев механизма подсчитывается по формулам в зависимости от вида движения каждого звена для всех принятых положений механизма. Кинетическая энергия звеньев определяется следующим образом:
а) для звеньев, совершающих поступательное движение (ползуны, штоки и т. д.)
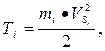

где mi — масса i-го звена;
VSi— скорость центра масс звена.
б) для звеньев, совершающих вращательное движение (кулисы, коромысла и т. д.)
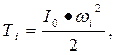
где wi — угловая скорость звена;
I0 — момент инерции относительно оси вращения (относительно центра шарнира).
Момент инерции I0 определяется:
IO = ISi + mi • l 2OSi,
где ISi— момент инерции звена относительно оси, проходящей через его центр масс;
l OSi — расстояние от центра масс звена до оси вращения (шарнира);
mi — масса звена.
в) для звеньев, совершающих сложное движение в плоскости (шатуны и т. д.);
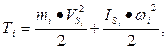 |
Определив кинетическую энергию каждого звена, вычисляют суммарную кинетическую энергию всех звеньев для каждого положения рычажного механизма; она подсчитывается как сумма кинетических энергий отдельных звеньев. Для рассматриваемого примера Т2 определяется:
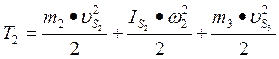
Таблица 2.4
Кинетическая энергия второй группы звеньев
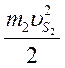
| 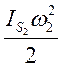
| 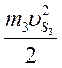
| Т2 | ||
| 0, 009 | 0, 003 | ||||
| 0, 012 | 0, 002 | 0, 008 | 2551, 17 | ||
| 0, 017 | 0, 0008 | 0, 02 | 4325, 9 | ||
| 0, 019 | 0, 02 | 4436, 82 | |||
| 0, 016 | 0, 0008 | 0, 013 | 3327, 6 | ||
| 0, 01 | 0, 002 | 0, 004 | 1885, 6 | ||
| 0, 009 | 0, 003 | ||||
| 0, 01 | 0, 002 | 0, 004 | 1885, 6 | ||
| 0, 016 | 0, 0008 | 0, 013 | 3327, 6 | ||
| 0, 019 | 0, 02 | 4436, 82 | |||
| 0, 017 | 0, 0008 | 0, 02 | 4325, 9 | ||
| 0, 012 | 0, 002 | 0, 008 | 2551, 17 | ||
По полученным данным строим диаграмму T2=f (j1), желательно, чтобы mT2=mT
Если равенство масштабов обеспечить не удаётся то диаграмма T2=f(j1) строится в произвольном масштабе. Выбираем mТ2 = 80 Дж/мм.
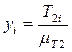 Ординаты графика для каждого положения получаем, переведя данные таблицы через масштабный коэффициент:
Ординаты графика для каждого положения получаем, переведя данные таблицы через масштабный коэффициент:
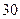
2.3.5 Диаграмма приращения кинетической энергии первой группы звеньев и определение момента инерции маховика.
DТ1=f(j1).
Изменение кинетической энергии DТ1 равно разности изменения кинетической энергии механизма вместе с маховиком DТ и кинетической энергии второй группы звеньев Т2.
Этот последний график при условии равенства масштабов mT=mT2 получают в результате графического вычитания графика Т2=f(j1) из графика DТ=f(j1). При графическом вычитании в отличие от графической разности графиков учитывается знак, например (—) — (+)= — (минус).
После указанных действий и соединения конечных точек полученных отрезков (ординат) плавной кривой получим график приращения критической энергии
DТ1 =f(j1).
При этом масштаб графика mDT1 =mT=mT2 .
Если диаграмму Т2=f(j1) построить в масштабе mT2 = mT невозможно, то умножив ординаты графика DТ=f(j1) на mT определяют реальные значения DТ для каждого положения механизма. Затем расчетным путем определяют значения DТ1 (DТ1 = DТ — Т2) и по ним строят график Т1=f(j1).
Таблица 2.5
Приращение кинетической энергии первой группы звеньев
| DТ | 110, 3 | 292, 7 | 402, 8 | 437, 1 | 428, 6 | 386, 9 | 337, 1 | 289, 1 | 240, 2 | 176, 3 | 80, 7 | |
| Т2 | 2551, 17 | 4325, 9 | 4436, 82 | 3327, 6 | 1885, 6 | 3327, 6 | 4436, 82 | 4325, 9 | 2551, 17 | |||
| DТ1 | -1331 | -2450, 9 | -4033, 2 | -4034 | -2890, 5 | -1457 | -944, 1 | -1548, 5 | -3038, 5 | -4149, 6 | -4149, 6 | -2470, 5 |
Диаграмму DТ1 =f(j1) строим в масштабе mT1 =60 Дж/мм
Ординаты графика определим 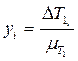
При определении приведённого момента инерции первой группы звеньев необходимо провести горизонтальные касательные к построенному графику DТ1 =f(j1) до пересечения их с осью ординат в точках К и D. Отрезок КD в масштабе mT1 величину DТ1наиб.
Тогда 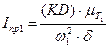
Iпр1=IМ – момент инерции маховика
2.3.6 Определение закона движения входного звена при установившемся режиме движения механизма
Закон изменения скорости звена приведения w1 при установившемся движении можно найти с помощью диаграммы изменения кинетической энергии первой группы звеньев DТ1=f(j1). Хотя этот способ является приближенным, но при малых коэффициентах неравномерности ошибка оказывается настолько малой, что в инженерных расчетах ею можно пренебречь. Из теории известно, что
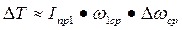
Если учесть, что Iпр1 и w1 являются величинами постоянными, то изменение угловой скорости Dw1 будет пропорционально изменению кинетической энергии DТ1. Таким образом, криваяDТ1=f(j1) будет представлять собой в другом масштабе закон изменения скорости Dw1 звена приведения. Если принять равенство соответствующих ординат Dw1 •mw= DТ1•mТ1, и то что mТ1 уже выбран при построениях, то масштабный коэффициент mw определяется следующим соотношением:
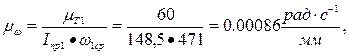 |
где mТ1[Дж/мм] - масштабный коэффициент кинетической энергии первой группы звеньев; Iпр1[кг·м2] - момент инерции первой группы звеньев; w1ср=wном[рад/с] - номинальное(заданное) значение угловой скорости; mw[рад·с-1/мм] - масштабный коэффициент угловой скорости.
Исходя из того, что 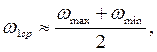
Делим отрезок KD пополам и проводим горизонтальную прямую соответствующую w1ср(заданному значению w1).
Для определения угловой скорости кривошипа в каждом положении механизма поступают следующим образом:
если отрезок Dw1 расположен выше прямой соответствующей w1ср (положение 6), w1 = w1ср + Dw1× mw,
если отрезок лежит ниже прямой w1ср (положение 3),
w1 = w1ср - Dw1× mw,
Для определения углового ускорения входного звена необходимо графически продифференцировать диаграмму w1 = f1(j1).
Дифференцирование проведем методом хорд. Кривую w1 =f (j1) на участках 0-1; 1-2; 2-3; и т.д. заменим хордами. Выбрав полюс Р на произвольном расстоянии Н слева от оси ординат диаграммы проведем лучи Р-1"; Р-2"; Р-3"..., параллельные соответствующим хордам ([0'- 1'] || [р-1" ]; [1'-2'] || [р-2" ]...). Отрезки 0-1"; 0-2"; 0-3"... на оси ординат будут пропорциональны средним значениям ej1(аналога углового ускорения кривошипа
ej1= dw1/dj1) на соответствующих участках. Снесем полученные точки на середины участков, на которых проведены хорды и соединим полученные точки плавной кривой.
Масштабный коэффициент определится:
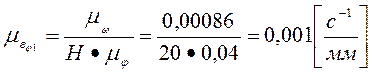 |
Угловое ускорение кривошипа определяется:
e1=ej1× w1ср
Для четвёртого положения механизма
e1 = (4 - 4*)× mej× w1ср
| Таблица 2.6 | Значения угловой скорости и углового ускорения кривошипа | 471, 002 | 0, 353 | |
| 470, 98 | 0, 301 | |||
| 470, 98 | -0, 188 | |||
| 470, 99 | -, 0325 | |||
| 471, 01 | -0, 283 | |||
| 471, 02 | ||||
| 471, 016 | 0, 283 | |||
| 470, 996 | 0, 363 | |||
| 470, 98 | 0, 179 | |||
| 470, 98 | -0, 254 | |||
| 471, 003 | -0, 349 | |||
| 471, 01 | 0, 085 | |||
| w1 | e1 |
Примечание:
(+) — угловое ускорение совпадает с направлением w1
(—) — угловое ускорение противоположно направлению w1
2.4. Кинетостатическое исследование механизма
Задача кинетостатики сводится к определению внутренних сил механизма, возникающих в его кинематических парах, движущего момента, приложенного к ведущему звену и необходимого для привода в движение механизма рабочей машины или момента сопротивления, приложенного к ведомому валу и преодолеваемого исследуемым механизмом двигателя. Необходимость определения усилий в кинематических парах связана с задачами расчета звеньев и элементов кинематических пар на прочность, создания оптимального варианта конструкции механизма, определения коэффициента полезного действия машины, ее уравновешивания на фундаменте и т. п. Движение всякого механизма происходит под действием внешних сил, к которым относятся движущие силы; силы полезного (производственного сопротивления), силы вредного сопротивления (трения, сопротивления среды и т. п.), силы веса звеньев и силы инерции их.
При исследовании тихоходной машины, звенья которой
движутся с незначительными ускорениями, определение усилий в кинематических парах можно произвести из условия равномерного движения механизма в целом и каждого его звена в отдельности. Расчетными уравнениями для каждого звена будут служить известные уравнения статики:
SРi =0,
SM(Рi) =0.
В быстроходных машинах ускорения звеньев могут достигать значительных величин и динамические усилия в кинематических парах механизма могут многократно превышать усилия от статического нагружения. В подобных случаях пренебрегать влиянием динамических нагрузок недопустимо. Одним из распространенных методов силового исследования механизма с учетом сил инерции является метод кинетостатики, основанный на использовании принципа Даламбера, сущность которого заключается в том, что каждое звено и группа Ассура могут рассматриваться в условном статическом равновесии, если к ним будут добавлены силы инерции.
В общем случае инерционная нагрузка на звено может быть сведена к главному вектору сил инерции, которой равен произведению массы звена mi на ускорение центра масс звена a Si.
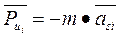
и направлен противоположно ускорению центра масс звена, и главному моменту сил инерции, равному по модулю произведению момента инерции звена относительно оси, проходящей через центр его масс ISi. на угловое ускорение звена e,
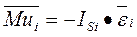
направленному противоположно угловому ускорению звена.
В итоге расчетные уравнения кинетостатики будут иметь вид
S(Pi+Pиi)=0
S[M(Pi)+M(Pиi)+Mиi]=0
Порядок кинетостатического исследования механизма заключается в последовательном рассмотрении условий равновесия групп Ассура, начиная с наиболее удаленной от ведущего звена, в результате которого определяются реакции связей, являющихся усилиями во внешних кинематических парах, возникающих вследствие освобождения группы от примыкающих звеньев механизма. Эта задача всегда разрешима в силу статической определимости групп Ассура. Действительно, считая, что для каждого звена можно составить 3 уравнения равновесия, а для звеньев 3n уравнений и учитывая, что реакция каждой кинематической пары 5 класса содержит 2 неизвестных (модуль и направление), то условие статической определимости получит вид
3n – 2p5 = 0.
Последнее выражение совпадает с известным условием существования групп Ассура.
Силовой расчет механизма проводится с учетом всех действующих внешних сил, за исключением сил трения, влиянием которых ввиду малости можно пренебречь. Наряду с заданной силой сопротивления и силами веса звеньев к известным силам относятся силы инерции и моменты пар сил
инерции.
Определим модули сил инерции звеньев и моментов пар сил инерции.
Pи1 = m1 · a S1 = 0, т.к. a S1=0
Mи1 = Iпр1 · e1 = 148, 5 · -0, 349 = -51, 8265 Н·м,
Pи2 = m2 · a S2 = 2, 9 ·17100 = 49590 Н,
Mи2 = IS2 · e2 = 0.06 · 24016, 9 = 1441 Н·м,
Pи3 = m3 · a B = 3, 5 · 17439 = 61036, 5 Н.
Приложены главные векторы сил инерции в центрах масс соответствующих звеньев и направлены противоположно вектору ускорения центра масс звена. Направление главных моментов сил инерции звеньев противоположно угловым ускорениям звеньев.
Силы веса звеньев определим:
G2 = m2 · g = 2, 9 · 9, 8 = 28, 49 Н,
G3 = m3 · g = 3, 5 · 9, 8 = 34, 3 Н.
Значение силы давления газов определим по индикаторной диаграмме: РВ = 10220 Н.
Силовой (кинетостатический) расчет начинаем с группы Ассура. Отсоединяем ее от механизма и вычерчиваем в масштабе m l =0, 002 м/мм. Покажем действующие на нее внешние силы и силы реакций, возникающих в разорванных связях. Действие отброшенной стойки заменим реакцией R43, которая направлена по перпендикуляру к направляющей и приложена в точке В, т. к. все силы, действующие на звено 3, проходят через ось шарнира В. Реакцию в шарнире А-R12 разложим на составляющие: Rn12 - нормальная составляющая, направленная вдоль звена АВ и
Rt12 - тангенциальная - по перпендикуляру к звену АВ.
Составляем уравнение равновесия для группы:
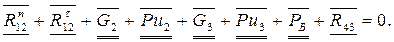
известны
В уравнении 3 неизвестных. Составляющую RT12 определим из уравнения моментов всех сил, действующих на звено 2 относительно точки В
SМ(В)=0

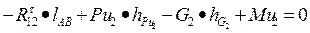

Для определения плеча силы опускаем перпендикуляр из точки В на линию действия силы 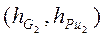 , замеряем их и умножаем на масштабный коэффициент m l:
, замеряем их и умножаем на масштабный коэффициент m l:
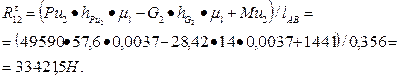 |
Если в результате расчета реакция RT12 получается со знаком минус, то выбранное направление следует изменить на противоположное.
После определения Rt12 в уравнении остаются
неизвестными величины сил Rn12 и R43, и по векторному уравнению можно построить векторный многоугольник сил. Выбираем для построения масштабный коэффициент сил mР =1012 Н/мм, тогда отрезки, изображающие силы на чертеже определятся делением величины силы на mР.
[Rt12] = Rt12/mР = 33421, 5/1012 = 33 мм.
Отложив векторы известных сил в соответствии с уравнением, из начала вектора Rt12 проводим линию действия вектора Rn12, a из конца Рс - линию действия R43. Точка пересечения этих направлений отмерит величины реакций.
Rn12 = [Rn12]·mP = 96, 79·1012 = 97951, 5 Н,
R43 = [ R34]·mP = 18, 8·1012 = 19025, 6 Н,
R12 = [R12]·mP = 96, 53·1012 = 97688, 4 Н.
Для определения реакции во внутренней кинематической паре в т. В рассмотрим равновесие звена 2.
Уравнение равновесия запишется в следующем виде:
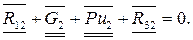
Для нахождения реакции R32 достаточно_на плане сил группы 2-3 соединить конец вектора Ри2 с началом R12. Полученный отрезок определит величину R32.
R32= [R32]·mp= 54, 17·1012= 54820 Н.
Заканчивается силовой анализ рассмотрением механизма первого класса, состоящего из ведущего звена и стойки, которые образуют между
собой вращательную кинематическую пару пятого класса.
Из условия статической определимости кинематической цепи следует, что под действием приложенных сил механизм 1 класса не находится в равновесии, т.к. при числе подвижных звеньев, равном единице, и числе кинематических пар 5 класса равном единице, число уравнений равновесия, которое мы можем составить, на единицу больше числа неизвестных.
3n – 2p5 = 3·1 – 2·1 = 1
Чтобы имело место равновесие, необходимо дополнительно ввести силу или пару сил, уравновешивающую все силы, приложенные к ведущему звену. Эта сила или момент пары сил носят название уравновешивающей силы (Р у) или уравновешивающего момента (Му).
Вычерчиваем в масштабе М l механизм 1 класса, прикладываем к звену 1 действующие силы и моменты сил: реакцию R21= - R12, приложенную в точке А, момент Ми1 направленный против e1, уравновешивающий момент М у.
Для определения Му состовляем уравнение моментов относительно точки О
SM(O) = 0
-R12·hR12+Mу– M и1 = 0
Mу = Mи1+R12 · [ hR12] · m l =
=-51, 83+97688, 4 · 20, 41 · 0, 0037 = 7685, 15 Н·м
Векторное уравнение сил, действующих на звено 1