
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определяем геометрические размеры зубчатой передачи
|
|
Радиусы начальных окружностей:
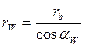
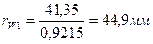
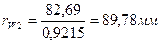
Радиусы окружностей вершин:
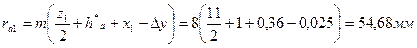
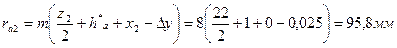
Радиусы окружностей впадин:
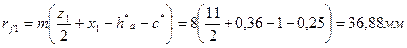
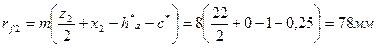
Толщины зубьев по делительной окружности:

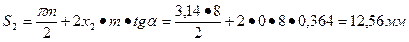
Проверка произведённого расчёта
a w = r a 1 + c*m + rf2 = 54, 68 + 0, 25 · 8 + 78 = 134, 68
a w = r a 2 + c*m + rf1 = 95, 8 + 0, 25 · 8 + 36, 88 = 134, 68
При несовпадении результатов проверки с ранее определённым значением а w необходимо произвести тщательную проверку расчёта.
Проверка на заострение
Определим толщину зуба окружности вершин,
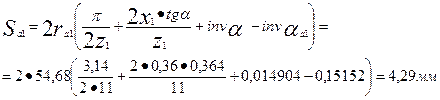
где 
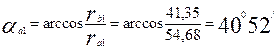


где 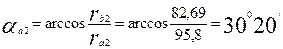
Для отсутствия заострения необходимо, чтобы 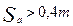
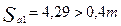
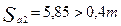

Определим коэффициент перекрытия
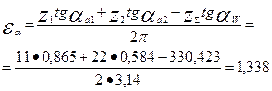
Синтез планетарного механизма
Синтез планетарного механизма заключается в подборе чисел зубьев его колёс таким образом, чтобы удовлетворить следующим условиям:
- обеспечить заданное передаточное отношение – подобрать числа зубьев зубчатых колёс так, чтобы передаточное отношение редуктора было равно требуемому или находилось бы в диапазоне его допустимых значений (±2%);
- условие соосности заключается в том, что оси центральных колёс и водила должны лежать на одной прямой;
- условие соседства требует, чтобы между окружностями выступов зубьев соседних сателлитов существовал зазор и оно определяет максимально возможное число сателлитов;
- условие сборки – условие равных углов между сателлитами- требует одновременного зацепления всех сателлитов с центральными колесами при симметричном расположении данного зацепления.
- условие правильного зацепления – условие отсутствия заклинивания и отсутствия интерференции зубьев. Числа зубьев зацепляющихся колёс должны удовлетворять условиям: Z3³ 17; Z4³ 20; Z5³ 85
На основании ранее изложенного для заданного механизма запишем:
- передаточное отношение

 (3.1)
(3.1)
- условие соосности:
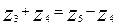 (3.2)
(3.2)
- условие сборки сателлитов
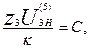 (3.3)
(3.3)
где 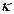 - число сателлитов
- число сателлитов
С- любое целое число;
- максимальное число сателлитов из условия соседства:
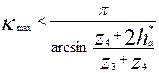 |
(3.4)
Из уравнения (3.1) получим
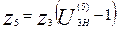 (3.5)
(3.5)
Подставив (3.1) в (3.2) получим:
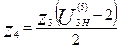 |
(3.6)
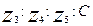
Соотношение
с учётом значений этих величин, выраженных формулами (3.3), (3.5) и (3.6), даёт общее уравнение для определения чисел зубьев однорядного планетарного редуктора:
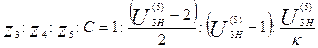 |
(3.7)
Если 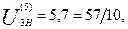 m=8 мм,
m=8 мм, 
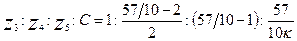 (3.7)
(3.7)
После вычисления получим:
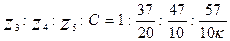 |
Умножим все члены правой части пропорции на 20, что обеспечит минимальные габариты механизма при отсутствии подрезания и заклинивания. Тогда:

Откуда Z3=20 Z4=37 Z5=94.
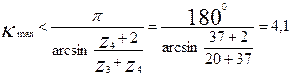 Максимально возможное число сателлитов из условия соседства
Максимально возможное число сателлитов из условия соседства

т.е. практически может быть 2, 3, 4.
По заданию к=3. Последний член пропорции 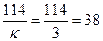
- целое число, т.е. условие сборки выполняется.