Поняття про теорію спадкової повзучості

Згідно сучасних уявлень, напруження, що виникають в реальних тілах, складаються з двох частин: перша складова залежить від деформації в даний момент часу t, друга - від деформацій, що існували в тілі протягом часу, що передував справжньому моменту часу - 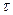. Час змінює структуру.

Теорія, що дозволяє визначати деформації в середовищі з урахуванням історії її навантаження, називається теорією спадкової повзучості.

Теорія спадкової зміни внутрішніх чинників з урахуванням «пам'яті» матеріалу про всі тимчасові структурні зміни, що виникають в процесі навантаження, і допускаюча лінійну залежність між напруженнями і деформаціями у будь-який момент часу, одержала назву теорії лінійної спадкової повзучості,

Теорія лінійної спадковості була запропонована Л. Больцманом з використанням математичного апарату інтегральних рівнянь В. Вольтера.

Відповідно до цієї теорії, деформації середовища під дією зовнішніх сил продовжуються і після їх прикладання (спадковість), при цьому деформації в кожен момент часу прямо пропорційні діючим в різні моменти часу напруженням (лінійність) сумуються, ростуть в часі (принцип суперпозиції).

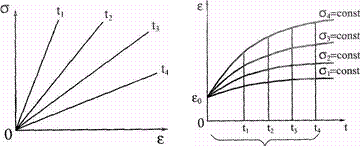
Проілюструємо вище викладене на наступному прикладі. Побудуємо криві повзучості g= 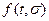при різних рівнях напруження (рис. 1, а). Потім в координатах « 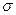- g» побудуємо графіки в моменти часу 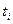(і=1, 2, 3...) (рис.1, б). Якщо ізохорні залежності, що вийшли при цьому, є прямими лініями (або близькими до них), то ми маємо справу з лінійним спадковим середовищем.

Повзучість матеріалів в теорії лінійної спадковості описується інтегральним рівнянням Вольтера другого роду

g (1)

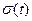де— і g 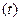- напруження і деформації в даний момент часу 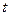, 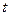- час, який передує моменту часу 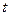; 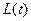- деяка функція, яка враховує вплив часу на деформації і напруження в тілі.

а) б)

Рис.1. Деформування в часі спадкового середовища

При 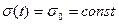із співвідношення (1) отримаємо рівняння повзучості деформацій

g 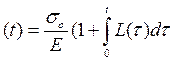(2)

Диференціюючи обидві частини рівняння (2) по часу, отримаємо вираз:

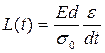
з якого слідує, що 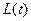являє собою функцію швидкості повзучості. Функцію ж 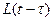називають ядром інтегрального рівняння Вольтера (1). Розв’язуючи це відносно 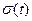, отримаємо,

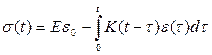(3)

При 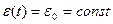з (3) отримаємо рівняння релаксації напружень

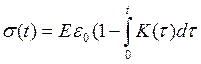(4)

Диференціюючи обидві частини (4) по , отримаємо вираз для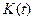

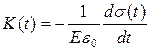
Функці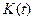ї і 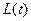взаємопов’язані і це дозволяє за однією з них знайти іншу. Функція 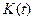називається резольвентою інтегрального рівняння Вольтера (2).

Рівняння повзучості (2) можна записати у вигляді

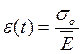
де 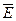- тимчасовий оператор, який визначається в результаті обробки експериментальних даних.

Ю.Н. Работнов показав, що задачу лінійної спадковості можна формально розглядати, як задачу теорії пружності, в якій замість пружних постійних Е і 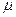необхідно використовувати їх тимчасові аналоги (інтегральні оператори) 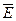і 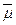. Ж.С. Ержанов встановив, що деформація ряду гірських порід до певного рівня навантаження відповідає рівнянню (2) з ядром повзучості у вигляді степеневої функції (ядро типу Абеля):

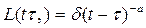
де 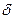і 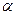- реологічні характеристики, отримані експериментально.

Інтегральне рівняння повзучості з ядром Абеля має наступний розв’язок

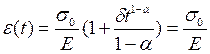(5)

Складність рішення задач методами теорії спадкової повзучості полягає в розшифровці тимчасових операторів.

Часто при постійності граничних умов для вирішення задач геомеханіки використовують метод змінних модулів, який полягає у тому, що замість інтегральних операторів 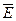і 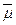використовують часові функці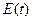ї і .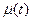

З виразу (5) слідує, що функція часу модуля деформації має вигляд

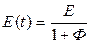
де Ф –функція повзучості, яка рівна

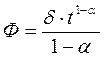
Функція часу для коефіцієнта Пуассона визначається виразом

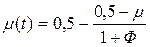
Слід відмітити, що використання теорії спадкової повзучості виправдане тільки в тому випадку, коли діюче напруження не перевищує тривалої міцності масиву.