
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Напруженому стані
|
|
Передумова про малий вплив проміжного по величині напруження на руйнування гірських порід є єдиною в теорії Мора, яка в основному не вимагає перевірки, оскільки цілком ґрунтується на експериментальних даних. Однак, аналітичний критерій міцності отримується шляхом підбору відповідного емпіричного виразу і його застосування обмежується власне кажучи тією областю напружених станів, у якій виконані експерименти.
Таким чином, експериментальний характер забезпечує досить точний опис граничного стану матеріалу, емпіричний же підбір умови міцності не дає можливості повною мірою скористатися цією перевагою. Тому цікавим є висновок аналітичного критерію теорії на основі аналізу процесу руйнування в локальній області твердого тіла, що може бути представлений наступним способом. Дотичні напруження, величина яких досить повно характеризується інтенсивністю напружень 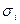 , розпушують матеріал шляхом здвигання, а під дією нормальних напружень, рівень яких визначається кульковим тензором I, відбувається розкриття тріщин.
, розпушують матеріал шляхом здвигання, а під дією нормальних напружень, рівень яких визначається кульковим тензором I, відбувається розкриття тріщин.
Ряд сучасних теорій міцності був отриманий на основі моделі руйнування твердих тіл із загальної функціональної залежності, яка об’єднує в одне співвідношення інтенсивності напружень і компоненти шарового тензора I:
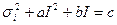 (5)
(5)
де а, b, c—деякі параметри, визначені з випробувань при найпростіших напружених станах:
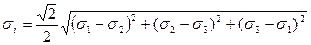 (6)
(6)
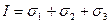 (7)
(7)
Наступна гіпотеза Мора, припустимо, що міцність матеріалу практично залежить тільки від тих членів рівняння (6) і (7), які визначають різницю і суму найбільшого і найменшого компонентів напружень. Тоді з (5) при 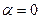 , отримаємо наступний вираз:
, отримаємо наступний вираз:
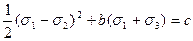 (8)
(8)
Параметри b і с визначимо з (8) в результаті вимірювань гірських порід при найпростіших напружених станах: при одноосному стисненні отримаємо
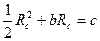 (9)
(9)
при одноосному розтягуванні
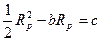 (10)
(10)
Розв’язуючи рівняння (9) і (10), знаходимо, що
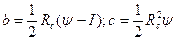 де
де 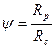 (11)
(11)
Підставивши значення параметрів (11) у відношенні (8), отримаємо наступну умову міцності
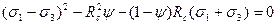 (12)
(12)
чи в загальному вигляді напруженого стану
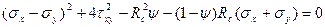 (13)
(13)
З рівняння (12) отримаємо
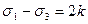 (14)
(14)
де
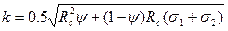 (15)
(15)
Відмітимо, що при осесиметричному розподіленні напружень 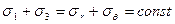 . З цього слідує, що вираз (14) є умовою міцності Треска-Сен-Венана. В загальному ж випадку напруженого стану перша частина умови (14) залежить від значень компонентів напруження.
. З цього слідує, що вираз (14) є умовою міцності Треска-Сен-Венана. В загальному ж випадку напруженого стану перша частина умови (14) залежить від значень компонентів напруження.
Для матеріалів, які однаково протидіють стисненню і розтяганню, 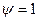 . В цьому випадку із виразу (14) отримаємо теорію Кулона.
. В цьому випадку із виразу (14) отримаємо теорію Кулона.
При 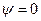 із (12) отримаємо наступний частковий вираз теорії міцності
із (12) отримаємо наступний частковий вираз теорії міцності
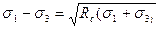 (16)
(16)
Позначимо відповідно максимальне дотичне напруження і величину, яка характеризує вид напруженого стану, як 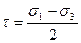 і
і 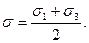 Тоді вираз (12) з врахуванням прийнятих позначень набуде вигляду
Тоді вираз (12) з врахуванням прийнятих позначень набуде вигляду
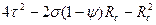
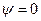 (17)
(17)
Залежність (17) в системі координат «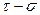 » являє рівняння параболи, що є опуклою і безперервною кривою.
» являє рівняння параболи, що є опуклою і безперервною кривою.
Залежність (17) в системі координат «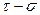 » являє рівняння параболи, що є опуклою і безперервною кривою.
» являє рівняння параболи, що є опуклою і безперервною кривою.
 У системі координат «
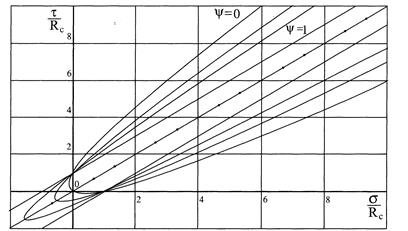
У системі координат «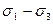 » рівняння ( 12 ) має вигляд параболи, рівно нахиленої до осей і відкритої зі сторони стискаючих напружень, що відповідає вимозі симетричності умови виникнення граничного напруженого стану (рис.4 ). Із збільшенням величини
» рівняння ( 12 ) має вигляд параболи, рівно нахиленої до осей і відкритої зі сторони стискаючих напружень, що відповідає вимозі симетричності умови виникнення граничного напруженого стану (рис.4 ). Із збільшенням величини 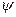 від 0 до 1 парабола витягається в сторону всебічного розтягання, що підтверджується дослідами Г.В. Ужика. І при
від 0 до 1 парабола витягається в сторону всебічного розтягання, що підтверджується дослідами Г.В. Ужика. І при 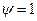 парабола перетворюється в дві рівнобіжні прямі, які відповідають теорії «енергії формозміни».
парабола перетворюється в дві рівнобіжні прямі, які відповідають теорії «енергії формозміни».
Рис. 4. Поверхні граничних станів за формулою (3.17)
Таким чином, отримана умова міцності відповідає вимогам постулату Друккера і відповідає сучасним уявленням про природу руйнування твердих тіл.
Руйнування крихких матеріалів досить добре описується теорією Гриффітса. Муррель показав, що в системі координат «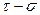 » основне рівняння теорії Гриффітса може бути представлене наступним чином
» основне рівняння теорії Гриффітса може бути представлене наступним чином
 (18)
(18)
Якщо в залежність (17) підставити, згідно Гриффітсу, 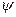 = 1/8 і порівняти її з залежністю (18), то виявиться, що аналітичні вирази двох теорій міцності, отримані на основі різних фізичних представлень про природу руйнування, є практично ідентичними.
= 1/8 і порівняти її з залежністю (18), то виявиться, що аналітичні вирази двох теорій міцності, отримані на основі різних фізичних представлень про природу руйнування, є практично ідентичними.
Умова міцності (12) при 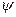 =1 була перевірена Баушингером, який показав, що вона добре описує процес руйнування пластичних матеріалів.
=1 була перевірена Баушингером, який показав, що вона добре описує процес руйнування пластичних матеріалів.
На рис.5 і рис.6 показана теоретична крива залежності (12) у системі безрозмірних координат (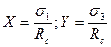 ) і результати випробувань гірських порід, одержані А.Н. Ставрогіним і X. Куком.
) і результати випробувань гірських порід, одержані А.Н. Ставрогіним і X. Куком.
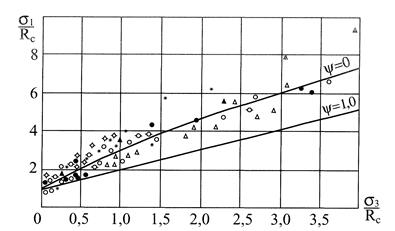 Рис. 5. Порівняння аналітичного критерію (12) з результатами іспитів гірських порід і бетону [3: о - вапняк,
Рис. 5. Порівняння аналітичного критерію (12) з результатами іспитів гірських порід і бетону [3: о - вапняк,  – аргіліт, ▲ - талькохлорит, -о- - мармур 1, + - діабаз, * - діорит,
– аргіліт, ▲ - талькохлорит, -о- - мармур 1, + - діабаз, * - діорит,
-☼ - алевроліт Д-19, піщаник Д-12, ● -бетон.
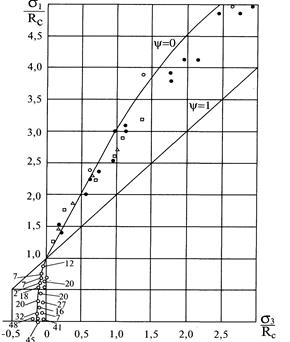
Рис. 6. Порівняння аналітичного критерію (12) з результатами випробувань гірських порід
Незважаючи на деяке наявне розкидання експериментальних точок, неминуче при випробуваннях структурно неоднорідних матеріалів, якими є гірські породи і бетони, з малюнків випливає, що запропонована умова міцності (12) досить добре описує процес їхнього руйнування при об'ємному стисканні і стисканні з розтяганням.
Із виразу (12) може бути отримана формула для приведення складного напруженого стану до простого одноосного. Вона має наступний вигляд:
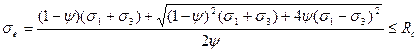 (19)
(19)
Тут 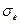 —еквівалентне напруження, тобто напруження, подібне одноосному напруженому стану.
—еквівалентне напруження, тобто напруження, подібне одноосному напруженому стану.
Використовуючи формулу (19) можна за допомогою коефіцієнта запасу міцності n оцінити ступінь небезпеки руйнування породного середовища для будь-якої точки однорідного породного масиву в околиці виробки, порівнюючи величину 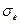 з межею міцності на одноосне стиснення Rc:
з межею міцності на одноосне стиснення Rc:
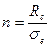
6 Напружено-деформований стан породних масивів. Початковий напружений стан зв’язаних породних масивів. Початковий напружений стан сипучих породних масивів. Характерні особливості прояву гірського тиску та задачі управління ним в очисних виробках. Прояви гірського тиску в очисних виробках за різних систем розробки родовищ. Напружено-деформований стан порід навколо очисної виробки. Зони опорного тиску і розвантаження.