Випробування гірських порід в складному напруженому стані

Математичне моделювання механічних процесів, що розвиваються навколо гірських виробок під дією сил гравітації і неотектоніки, тим ближче відповідають дійсності, чим краще прийнята теорія міцності відображає природу і характер руйнування породного середовища. Аналіз сучасних уявлень про міцність твердих тіл показує, що єдиної теорії руйнування, придатної для практичного застосування, на даний момент немає, не дивлячись на численні аналітичні і експериментальні дослідження, що проводяться в цій області.

В інженерній практиці найбільшого поширення набули феноменологічні теорії міцності. Не розкриваючи причин, що лежать в основі процесу руйнування, вони достатньо добре відображають поведінку матеріалів при їх граничній деформації в складному напруженому стані. Інженерні теорії міцності не універсальні, вони годяться, в основному, для порівняно вузького класу випробуваних матеріалів в межах штучно створюваних напружених станів. Цим значною мірою пояснюється досить велика їх кількість: добре описуючи процес руйнування одних твердих тіл, вони непридатні для інших, відмінних за структурою.

Однією з найпоширеніших в механіці гірських порід є теорія міцності Мора і її модифікації, яка повністю базується на експериментальних даних. Дані одержують при випробуваннях зразків гірських порід в об'ємному напруженому стані. Один з приладів подібного роду був сконструйований Н. Карманом для перевірки теорії міцності О. Мора. Прилад має наступну будову (рис.2).

В камеру високого тиску (3) поміщають зразок гірської породи циліндричної форми (2), обернутий алюмінієвою або мідною фольгою. Зусилля Р₁ передається осьовим плунжером (1) від пресу, на якому розміщують прилад. Зусилля, - Рз створюється масляним насосом за допомогою плунжера гідромультиплікатора (4). Таким чином, до торців зразка прикладене навантаження Р₁, а до бокової поверхні — Р₃. В зразку, відповідно, виникають напруження 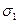і .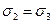

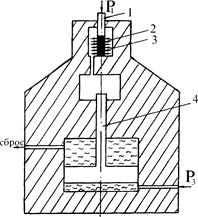
Рис.2. Прилад Кармана:

1—осьовий плунжер; 2—зразок гірської породи;

3—камера високого тиску;

4—плунжер гідрромультиплікатора

Зразок доводять до руйнування і за наслідками випробувань будують так звані граничні круги Мора (рис.3.) в системі координат «».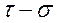

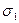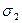Для цього, в самому загальному випадку, на осі відкладають нормальні напруження і та 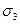(рис.3, а). На відрізках 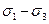, 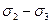і 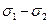як на діаметрах, будують граничні для даного напруженого стану круги Мора.

Прилад Кармана дозволяє моделювати об'ємний напружений стан з наступними компонентами напружень: 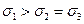. Подальші експерименти на подібних приладах, але дозволяючи вже реалізувати схему навантаження зразка кубічної форми, коли Р₁ 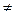Р₂ 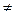Р₃ дозволили довести, що вплив проміжного за величиною навантаження 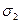не перевищує 10% і знаходиться в межах точності вимірювань. Таким чином, міцність гірських порід визначається, перш за все різницею найбільшого і найменшого напружень.

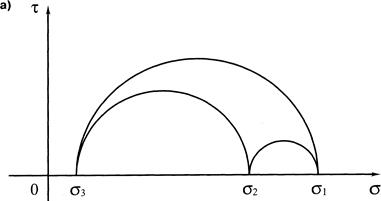
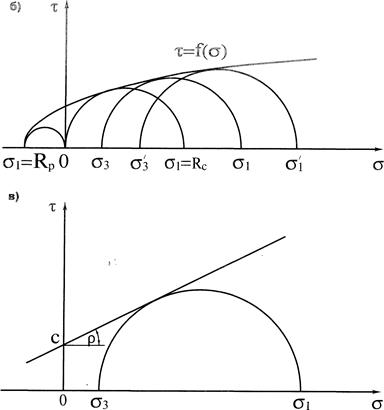
Рис.3. Графічна інтерпретація об’ємного напруженого стану:

а) вплив величини 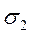; б) криволінійна огинаюча кругів Мора;

в)прямолінійна огинаюча кругів Мора.

Граничні круги Мора, побудовані для випадку, коли 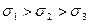показані на рис.3, а. Таких кругів, міняючи величину головних напружень, можна побудувати як завгодно багато. З’єднуючи круги плавною кривою, одержують згинаючу 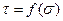, яка розділяє область небезпечних (вище кривої) і безпечних (нижче кривої) станів. Таку криву часто називають паспортом міцності матеріалу. Вона показана на рис.3, б.

В ході експериментів Н. Карман підтвердив можливість практичного використовування теорії міцності О. Мора і довів високу її надійність.

Для вирішення пружно-пластичних задач огинаючу граничних кругів в теорії міцності О.Мора необхідно апроксимувати якимсь рівнянням. Такі описи є у вигляді гіперболи, експоненти, циклоїди.

Нерідко криволінійну огинаючу замінюють прямолінійною, яка на осі 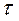відсікає відрізок, рівний С, і нахилена до осі 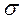під кутом 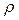, рівним величині кута внутрішнього тертя (рис.3, в). Слід зазначити, що заміна криволінійної огинаючої прямої є грубим спрощенням, що не має під собою фізичного обґрунтування.