Графическое изображение вариационных рядов

Анализ рядов распределения предполагает их графическое изображение. Для этой цели строят графики – полигон, гистограмму, кумуляту и огиву распределения.

Полигон используется при графическом изображении дискретных вариационных рядов. Для его построения на оси абсцисс откладывают варианты признака х_i, а на оси ординат – их частоты f_i или частости w_i. Полученные на пересечении абсцисс и ординат точки последовательно соединяют и получают ломаную линию, называемую полигоном частот, или эмпирической кривой распределения.

Для примера по данным табл. 3.4 представлен полигон распределения туристских фирм по числу сотрудников (рис. 3.2).

Рис 3.2. Полигон распределения

Замечание. Полигон часто замыкается. Для этого крайние точки соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе от 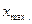и

Гистограмма используется при графическом изображении интервальных вариационных рядов. Для построения гистограммы на оси абсцисс откладывают границы интервалов признака х_i, а частоты f_i изображаются прямоугольниками, построенными на соответствующих интервалах с высотой в масштабе оси ординат. Высота столбиков должна быть пропорциональна частотам f_i или частостям w_i. В результате гистограмма представляет собой ряд сомкнутых прямоугольников, основаниями которых служит величина интервалов значений х_i, а высотой – частота f_i или частость w_i. График гистограммы построен по данным табл. 3.5 и представлен на рис. 3.3.

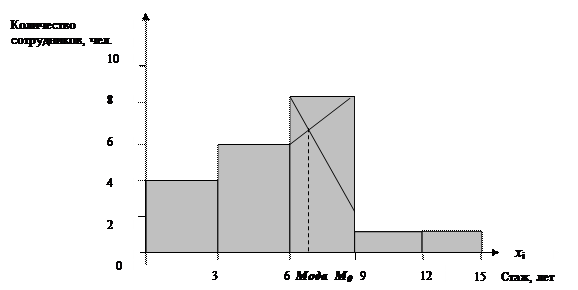
Рис. 3. 3. Гистограмма распределения сотрудников туристского предприятия по стажу работы

В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения или , так как в этом случае именно плотность дает представление о заполненности каждого интервала.

Замечание. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями.

Замечание. С помощью гистограммы графически можно определить приближенное значение моды М₀. Для этого правую вершину наибольшего прямоугольника соединяют прямой линией с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых является модой распределения. На рис. 3.3 прямые линии, соединяющие вершины прямоугольников, и перпендикуляр из точки их пересечения обозначены пунктирными линиями. Точное значение моды в случае интервального ряда определяется по специальной формуле (см. § 5.3).

В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята). Для ее построения следует рассчитать накопленные частоты или частости. При помощи кумуляты изображается ряд накопленных частот. При этом на оси абсцисс откладываются варианты х_i или верхние границы интервалов, а на оси ординат - соответствующие накопленные частоты F_i (или частости w_i). В верхних границах интервалов проводят перпендикуляры к оси абсцисс. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумулятивную кривую. Она начинается в точке нижней границы первого интервала (с частотой, равной нулю) и заканчивается в точке, соответствующей общей сумме частот.

На основе табл. 3.5 построена кумулята распределения сотрудников туристского предприятия по стажу работы (рис. 3.4).

Рис. 3.4. Кумулята распределения сотрудников туристского предприятия по стажу работы

Изображение вариационного ряда в виде кумуляты целесообразно в следующих случаях: 1) при сравнении вариационных рядов; 2) при наблюдении за процессом концентрации изучаемого явления (например, для анализа концентрации производства).

Замечание. С помощью кумуляты графически можно найти приближенное значение медианы M_{е .} Для этого на оси у находят точку . Через нее проводят прямую, параллельную оси х, до пересечения с кумулятой. Абсцисса точки пересечения является медианой. На рис. 3.4 показаны пунктирные линии, определяющие медиану. Точное значение медианы в случае интервального вариационного ряда определяется по специальной формуле (см. §. 5.3).

Если поменять местами оси координат, то есть, на оси х откладывать накопленные частоты F_i (или частости w_i), а на оси y – варианты х_i, то построенная на них кумулятивная кривая называется огивой.

При оценке степени концентрации (концентрации производства, капитала и др.) используется разновидность кумулятивной кривой – кривая Лоренца. График используется для анализа концентрации признака в тех или иных группах совокупности (для характеристики процессов концентрации, дифференциации и т.д.). При этом рассматривают параллельное изменение нарастающих долей единиц совокупности и нарастающих долей значений признака в общем объеме.

При построении на оси х откладывают накопленные частости (p_i) объема совокупности, а на оси у – накопленные частости значений признака (q _i) в общем объеме. Наносятся точки в соответствии с накопленными значениями двух рядов. Соединив точки, получают кривую, характеризующую степень неравномерности распределения. Если распределение является строго равномерным, то первые 10 % единиц обладают 10 % объема признака, первые 20 % единиц - соответственно 20 % объема признака и т.д. Это распределение отображается прямой, соединяющей нижний левый угол графика с правым верхним углом (диагональ четырехугольника), и называется линией равномерного распределения. Чем сильнее концентрация изучаемого признака (чем больше фактическое распределение двух показателей отклоняется от равномерного), тем больше кривая Лоренца отклоняется от линии равномерного распределения и наоборот.

На рис. 3.5 представлена кривая Лоренца распределения выручки по предприятиям региона (см. графы 6 и 9 табл. 3.6).

Рис. 3.5. Кривая Лоренца для распределения выручки туристских предприятий

Значит, чем больше это удаление (вогнутость), тем выше концентрация изучаемого показателя (в нашем случае – величины выручки) в определенных группах единиц (в нашем случае – в крупных предприятиях). Кривая степени концентрации может сколько угодно приближаться к линии равномерного распределения, но никогда ее не пересечет.

Для количественного измерения степени концентрации определенного суммарного показателя по выделенным группам единиц совокупности применяются следующие показатели:

§ коэффициент Джини;

§ коэффициент Лоренца;

§ коэффициент Герфиндаля.