
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовой задачи. Выполнил(а) студент(ка) I курса
|
|
Контрольная работа
По дисциплине
«Математика»
Вариант___
Выполнил(а) студент(ка) I курса
очной формы обучения
___________ ___________________
подпись Ф.И.О. студента
Проверила преподаватель
_______________/Кирдяпкина Н.В./
Дата_______________________Отметка о зачете________________
Приложение 2
Список использованной литературы
1. Высшая математика для экономистов: Учебник для вузов/под ред. Проф. Кремера Н.Ш. –2-е изд., перераб. и доп. –М.: Юнити, 2001
2. Черняк А.А., Доманова Ю.А. Сборник задач по высшей математике с демонстрационными примерами: Учебно-методическое пособие. – Мн.: МИТСО, 2002. – 96 с.
3. Шипачев В.С. Высшая математика.Учебник для вузов. –5-е изд. –М.: Высш. шк., 2002
Задание 1. Даны векторы  . Показать, что эти векторы образуют базис и найти координаты вектора
. Показать, что эти векторы образуют базис и найти координаты вектора  в этом базисе:
в этом базисе:
1.  (3; 1; 3),
(3; 1; 3), 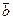 (2; 1; 0),
(2; 1; 0),  (1; 0; 1),
(1; 0; 1),  (4; 2; 1).
(4; 2; 1).
2. 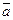 (10; 3; 1),
(10; 3; 1), 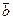 (1; 4; 2),
(1; 4; 2),  (3; 9; 2),
(3; 9; 2),  (19; 30; 7).
(19; 30; 7).
3. 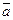 (2; -1; 11),
(2; -1; 11), 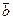 (1; 1; 0),
(1; 1; 0),  (0; 1; 2),
(0; 1; 2),  (2; 5; 3).
(2; 5; 3).
4. 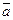 (8; 2; 3),
(8; 2; 3), 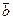 (4; 6; 10),
(4; 6; 10),  (3; -2; 1),
(3; -2; 1),  (7; 4; 11).
(7; 4; 11).
5. 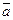 (1; -2; 3),
(1; -2; 3), 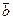 (4; 7; 2),
(4; 7; 2),  (6; 4; 2),
(6; 4; 2),  (14; 18; 6).
(14; 18; 6).
6. 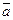 (3; 1; 8),
(3; 1; 8), 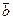 (0; 1; 3),
(0; 1; 3),  (1; 2; -1),
(1; 2; -1),  (2; 0; -1).
(2; 0; -1).
7. 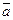 (2; 4; 1),
(2; 4; 1), 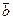 (1; 3; 6),
(1; 3; 6),  (5; 3; 1),
(5; 3; 1),  (24; 20; 6).
(24; 20; 6).
8. 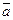 (-1; 7; -4),
(-1; 7; -4), 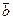 (-1; 2; 1),
(-1; 2; 1),  (0; -3; 2),
(0; -3; 2),  (2; 1; -1).
(2; 1; -1).
9. 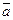 (4; 7; 8),
(4; 7; 8), 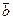 (9; 1; 3),
(9; 1; 3),  (2; -4; 1),
(2; -4; 1),  (1; -13; -13).
(1; -13; -13).
10. 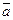 (2; 7; 5),
(2; 7; 5), 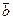 (1; 0; 1),
(1; 0; 1),  (1; -2; 0),
(1; -2; 0),  (0; 3; 1).
(0; 3; 1).
11. 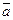 (3; 7; 2),
(3; 7; 2), 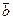 (2; 3; 4),
(2; 3; 4),  (6; 2; 2),
(6; 2; 2),  (3; -1; 2).
(3; -1; 2).
12. 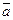 (0; 1; 1),
(0; 1; 1), 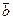 (2; 3; 4),
(2; 3; 4),  (0; 0; 1),
(0; 0; 1),  (-1; -2; -4).
(-1; -2; -4).
13. 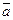 (-2; 0; -2),
(-2; 0; -2), 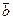 (0; -1; 1),
(0; -1; 1),  (-2; 0; -3),
(-2; 0; -3),  (-1; 1; -3).
(-1; 1; -3).
14. 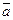 (0; -1; -3),
(0; -1; -3), 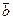 (0; 1; 0),
(0; 1; 0),  (-2; 1; -4),
(-2; 1; -4),  (-1; 1; -3).
(-1; 1; -3).
15. 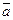 (-2; -2; -3),
(-2; -2; -3), 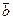 (-2; 1; 1),
(-2; 1; 1),  (-2; -2; 2),
(-2; -2; 2),  (-1; 1; 3).
(-1; 1; 3).
16. 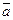 (2; -2; 0),
(2; -2; 0), 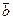 (3; 0; 1),
(3; 0; 1),  (4; -2; 0),
(4; -2; 0),  (3; -1; 1).
(3; -1; 1).
17. 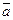 (2; -2; 4),
(2; -2; 4), 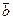 (3; 1; -1),
(3; 1; -1),  (-4; 5; 2),
(-4; 5; 2),  (8; -1; 6).
(8; -1; 6).
18. 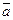 (3; 4; 1),
(3; 4; 1), 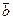 (5; 8; -1),
(5; 8; -1),  (6; -1; 4),
(6; -1; 4),  (5; -1; 3).
(5; -1; 3).
19. 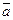 (-3; 1; 4),
(-3; 1; 4), 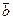 (7; 1; -5),
(7; 1; -5),  (8; 1; 6),
(8; 1; 6),  (-1; 2; 4).
(-1; 2; 4).
20. 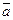 (-3; 8; 2),
(-3; 8; 2), 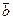 (5; 9; -4),
(5; 9; -4),  (6; 1; 8),
(6; 1; 8),  (-2; -3; -4).
(-2; -3; -4).
Решение типовой задачи.
Даны векторы  (2; -1; 3),
(2; -1; 3),  (1; 0; 2),
(1; 0; 2), 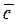 (3; 1; 1). Показать, что эти векторы образуют базис и найти координаты вектора
(3; 1; 1). Показать, что эти векторы образуют базис и найти координаты вектора  (0; -2; 4) в этом базисе.
(0; -2; 4) в этом базисе.
Решение. В трехмерном векторном пространстве любая тройка линейно независимых векторов образует базис. Поэтому необходимо доказать линейную независимость векторов  . Кроме того, чтобы представить вектор
. Кроме того, чтобы представить вектор 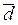 в виде линейной комбинации векторов
в виде линейной комбинации векторов  , необходимо решить систему линейных уравнений
, необходимо решить систему линейных уравнений 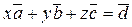 . Решим эту систему методом Гаусса. Одновременно выясним, являются ли векторы
. Решим эту систему методом Гаусса. Одновременно выясним, являются ли векторы  линейно независимыми (векторы
линейно независимыми (векторы  линейно независимы, если и только если система
линейно независимы, если и только если система  имеет единственное решение). Итак, составим расширенную матрицу данной системы уравнений и элементарными преобразованиями приведем ее к эквивалентному виду, содержащему базис переменных:
имеет единственное решение). Итак, составим расширенную матрицу данной системы уравнений и элементарными преобразованиями приведем ее к эквивалентному виду, содержащему базис переменных:

Вторая матрица получена из первой путем поочередного умножения второй строки на 2, 3 и прибавлением соответственно к первой и третьей строкам; третья матрица получена из второй прибавлением к третьей строке первой, умноженной на –2; четвертая матрица получена из третьей умножением второй строки на –1 и третьей строки на –1/6; и наконец, последняя матрица получена прибавлением ко второй строке третьей и к первой строке третьей, умноженной на –5.
Итак, х2 =1, х1 =1, х3 =-1.
Поскольку это единственное решение, то векторы  , образуют базис, в котором вектор
, образуют базис, в котором вектор  представим в виде
представим в виде 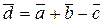 .
.
Задание 2. Найти матрицу  и
и 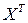 , если
, если
1. A =  , B =
, B =  , C =
, C =  .
.
2. A =  , B =
, B = 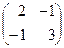 , C =
, C =  .
.
3. A =  , B =
, B =  , C =
, C =  .
.
4. A =  , B =
, B =  , C =
, C =  .
.
5. A =  , B =
, B = 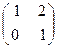 , C =
, C = 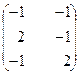 .
.
6. A =  , B =
, B =  , C =
, C =  .
.
7. A =  , B =
, B =  , C =
, C =  .
.
8. A = 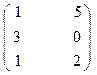 , B =
, B =  , C =
, C =  .
.
9. A =  , B =
, B =  , C =
, C = 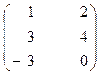 .
.
10. A =  , B =
, B =  , C =
, C =  .
.
11. A = 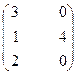 , B =
, B =  , C =
, C =  .
.
12. A =  , B =
, B = 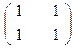 , C =
, C = 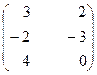 .
.
13. A =  , B =
, B =  , C =
, C =  .
.
14. A =  , B =
, B =  , C =
, C =  .
.
15. A =  , B =
, B = 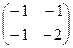 , C=
, C=  .
.
16. A = 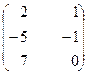 , B =
, B =  , C =
, C =  .
.
17. A =  , B =
, B =  , C =
, C =  .
.
18. A = 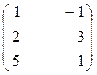 , B =
, B =  , C =
, C =  .
.
19. A =  , B =
, B = 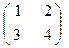 , C =
, C =  .
.
20. A =  , B =
, B = 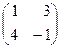 , C=
, C= 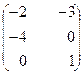 .
.