Сумма ряда

Постановка задачи. Найти сумму ряда

,

где – целые числа.

План решения.

Суммой ряда называется предел последовательности его частичных сумм 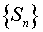, т.е.

,

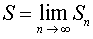где .

1. По условию задачи

.

Если корни знаменателя отличаются на целое число, т.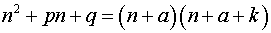е. , где – натуральное число, то члены последовательности частичных сумм ряда легко найти, т.к. в выражении многие слагаемые взаимно уничтожаются.

2. Раскладываем общий член ряда на элементарные дроби:

.

3. Находим -ю частичную сумму ряда:

,

сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле .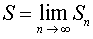

Замечание 1. Если коэффициент при не равен единице, но равен квадрату целого числа, то все выполняется аналогично.

Замечание 2. Если суммирование ряда начинается не с 1, а с некоторого номера 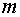, то -я частичная сумма ряда будет .

Задача. Найти сумму ряда.

.

Сумма ряда:

,

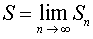где – сумма первых членов ряда.

Представим ряд в виде:

.

Тогда

Сумма ряда

.