Решение типовой задачи. Решить систему уравнений матричным методом.

Решить систему уравнений матричным методом.

Решение. Обозначим через A матрицу из коэффициентов исходной системы, через B – столбец из свободных членов, а через X – столбец из неизвестных, т.е.

, , .

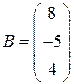Таким образом исходную систему можно записать в матричном виде AX=B.

Определитель , поэтому для матрицы A существует обратная матрица A^-1. Умножив обе части равенства AX=B слева на матрицу A^-1, получаем 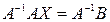. Так как , EX=X, то равенство 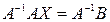примет вид X=A^-1B.

Эта формула является матричной записью решения исходной системы.

Найдем матрицу A^-1, обратную матрице A, с помощью элементарных преобразований:

откуда .

Тогда искомое решение определяется равенством:

.

Задание 5. Найти сумму ряда.

1.	2.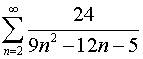
3.	4.
5.	6.
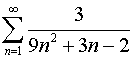
7.	8.
9.	10.
11.	12.
13.	14.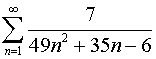
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.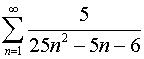
27.	28.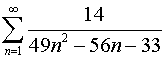
29.	30.
31.