
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовой задачи. Вычислить определитель четвертого порядка
|
|
Вычислить определитель четвертого порядка
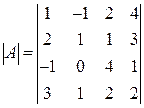 , разлагая его по элементам первого столбца.
, разлагая его по элементам первого столбца.
Решение. Преобразуем определитель, не меняя его величины. Прибавим к второй строке первую, умноженную на (-2), к третьей первую, из четвертой вычтем первую, умноженную на 3, получим
 .
.
Теперь разложим полученный определитель по элементам первого столбца:
 ,
,
где A11, A21, A31, A41, – алгебраические дополнения элементов a11, a21, a31, a41.
Последний определитель вычисляем по правилу треугольников:

Его можно вычислить также разложением по элементам первого столбца, предварительно прибавив вторую строку, умноженную на 3, к первой строке, вторую строку, умноженную на 4 – к третьей строке:

Заметим, что вычисления определителя путем разложения его по строке (столбцу) тем эффективнее, чем больше нулей в строке (столбце). Нули в строке (столбце) можно получить, применяя преобразования, не меняющие величины определителя.
Задание 4. Решить систему линейных уравнений матричным методом (с помощью обратной матрицы):
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|