На курсовую работу по дисциплине

" Статистическая динамика"

Тема: Анализ точности системы стабилизации угла курса осесимметричного ЛА при шуме в управляющем сигнале

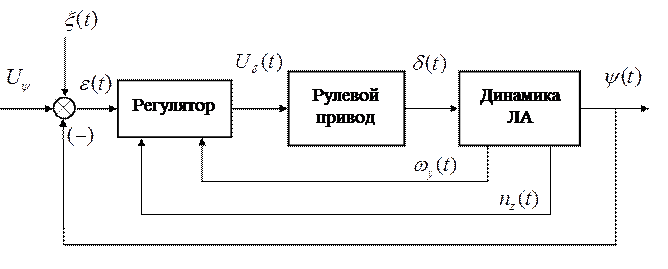
1. Функциональная схема системы:

курса. Сигнал поступает из системы наведения ЛА;

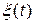- шум в управляющем сигнале - стационарный случайный процесс;

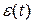- сигнал ошибки по регулируемой координате (углу курса ЛА);

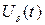- команда управления рулями;

- угол поворота рулей;

- перегрузка ЛА по его поперечной оси z;

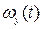- угловая скорость вращения ЛА относительно его поперечной оси y;

- угол курса ЛА.

2. Математические модели компонентов системы:

2.1. Регулятор

.

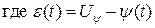2.2. Рулевой привод

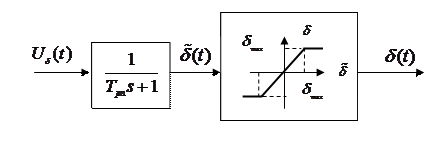
2.3. Динамика ЛА описывается следующими передаточными функциями ЛА как объекта управления в угловом движении

- ускорение силы тяжести на поверхности Земли.

3. Входы и выход системы:

= const – управляющий сигнал по нормальной перегрузке ЛА;

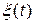- шум в управляющем сигнале - стационарный случайный процесс;

- выход – угол курса ЛА.

4. Начальные условия движения системы: нулевые.

5. Возможные методы анализа:

а) Частотный метод - для оценки математического ожидания и дисперсии 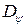выхода при линейном варианте системы (без учета нелинейности в рулевом приводе) в установившемся режиме.

б) Метод уравнений моментов при линейном варианте системы (без учета нелинейности в рулевом приводе) в переходном и в установившемся режимах.

б) Метод Монте-Карло (без учета и с учетом указанной нелинейности).

6. Требуется:

а) Для линейного варианта системы рассчитать двумя методами (методом Монте-Карло и одним из аналитических методов, указанныхв варианте задания), математическое ожидание и дисперсию 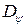угла курса ЛА в установившемся режиме. Сравнить полученные решения.

б) Для нелинейного варианта системы рассчитать методом Монте-Карло и построить графики зависимостей и от варьируемого параметра при изменении этого параметра в заданном диапазоне 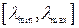с заданным шагом . Наименование варьируемого параметра, диапазон и шаг его варьирования указаны в исходных данных для заданного варианта задания.

7. Исходные данные: указаныв таблице исходных данных к вариантам задания 1.

Характеристики формирующих фильтров для имитации окрашенных шумов указаны в таблицах 1 и 2.