
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения линейных дискретных колебательных систем Вопрос 1
|
|
Общим подходом к моделированию колебательных систем, в котором определены кинетическая и потенциальная энергии является формализм Лагранжа. В радиотехнических системах, которые можно представить соединением конечного числа элементов (активных и пассивных), оказывается полезным метод уравнений Кирхгофа (основан на том, что токам и напряжениям ставится в соответствие их изображения по Лапласу):

| (1.1) |
Свойства преобразования Лапласа:
1. Линейность:  . .
| (1.2) |
2. Правило сдвига:  . .
| (1.3) |
3. Дифференцирование: 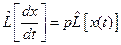 . .
| (1.4) |
4. Интегрирование:  . .
| (1.5) |
Для линейных двухполюсников, общий вид которых представлен на рис.1, вводят понятия операторного сопротивления и операторной проводимости:
 и
и  ,
,
где I (p) и U (p) - изображения по Лапласу тока и напряжения соответственно, т.е.
 ,
,  .
.
Определим теперь операторные сопротивления Z и проводимости Y для типовых идеальных двухполюсников, пользуясь свойствами (1.2), (1.4) и (1.5).
 Рис. 1. Двухполюсник.
Рис. 1. Двухполюсник.
| Для резистора: Ri (t) = u (t) Û U (p) = RI (p), тогда Z = R, Y = 1/ R.
Для конденсатора:  Û I (p) = CpU (p), Û I (p) = CpU (p),  , Y = Cp.
Для индуктивности: , Y = Cp.
Для индуктивности:  Û U (p) = LpI (p), Z = Lp, Û U (p) = LpI (p), Z = Lp,  . .
|
Запишем также законы Кирхгофа в операторной форме:
| 1. Сумма токов, сходящихся в узле, равна нулю, т. е. |  Рис. 2. Иллюстрация к первому правилу Кирхгофа: узел.
Рис. 2. Иллюстрация к первому правилу Кирхгофа: узел.
|

| (1.6) |
| 2. Сумма напряжений на всех элементах произвольного замкнутого контура равна нулю (в операторной форме): | |

| (1.7) |
Рассмотрим последовательный и параллельный колебательные контура (см. рис. 3, рис. 4). Можно записать следующие уравнения (для последовательного колебательного контура), которые следуют из закона Ома:

или (если избавиться от p в знаменателе)
 .
.
Теперь, применяя свойства преобразования Лапласа, запишем последнее уравнение в виде
 .
.
 Рис. 3. Последовательный колебательный контур.
Рис. 3. Последовательный колебательный контур.
|  Рис. 4. Параллельный колебательный контур.
Рис. 4. Параллельный колебательный контур.
|
Для параллельного колебательного контура проделаем аналогичные процедуры: из закона Ома, а также правила сложения сопротивлений при параллельном соединении следует, что
 .
.
Приведя к общему знаменателю, получим: 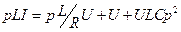 . Перейдём теперь от уравнения в операторном виде к дифференциальному уравнению:
. Перейдём теперь от уравнения в операторном виде к дифференциальному уравнению:

Таким образом, можно получить некоторые операторы:
 . .
| (1.8) |
Эти операторы, в общем случае, интегрально-дифференциальные, но это не очень удобно, поэтому мы и приводили уравнения к общему знаменателю и получали при этом уравнения вида
 , ,
| (1.9) |
где  и
и  - линейные дифференциальные операторы, т. е.
- линейные дифференциальные операторы, т. е.
 и
и  .
.
Применим преобразование Лапласа к (1.9) с учётом свойств (1.2) и (1.4):
 .
.
Формально можно найти операторное сопротивление системы:
 , ,
| (1.10) |
т. е. операторное сопротивление есть дробно-рациональная функция.
Пусть теперь на линейную систему производится гармоническое воздействие u (t) = U cos(wt + j). Будем считать, что параметры системы (an и bm) постоянны, т. е. у нас есть система с постоянными параметрами. Из свойств линейных систем с постоянными параметрами вида (1.9) следует, что в установившемся режиме реакция системы на гармонический сигнал будет гармоническим сигналом той же частоты, т. е. i (t) = I cos(wt + y). Воспользуемся методом комплексных амплитуд: поставим во взаимооднозначное соответствие сигналам их комплексные амплитуды, тогда
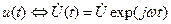 , где
, где  ;
;
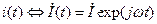 , где
, где  .
.
Для линейных операторов выполняется соотношение:
 ,
,
с помощью которого можно записать (1.9) в виде:
 ,
,
и тогда найдём комплексное сопротивление как отношение комплексных амплитуд:
 . .
| (1.11) |
Таким образом, мы нашли сопротивление операторным методом и методом комплексных амплитуд. Операторный метод предполагает, что сигнал начался в момент времени t = 0. Он справедлив как в установившемся, так и в переходном режиме. В методе комплексных амплитуд предполагается, что сигнал начался давно (установившийся режим).
Рассмотрим для примера составление уравнения для резонансного усилителя (см. рис. 5). Полевой транзистор представляет собой источник тока, и приложенное напряжение заставляет его генерировать ток. Таким образом, часть резонансного усилителя, которая на рис. 5 обведена штриховой линией, можно принять за источник тока и перерисовать усилитель в эквивалентном виде, который представлен на рис. 6. Резисторы R 1 и R 2 описывают потери в резонансных контурах L 1 C 1 и L 2 C 2. Второй каскад на транзисторе T2 усиливает напряжение в k раз, т. е. u 3 = ku2.
Выберем в качестве обобщённых координат токи i 1 и i 2. Запишем второе правило Кирхгофа для первого и второго контуров на рис. 6.

Умножим второе уравнение на pC 1, а третье на pC 2:
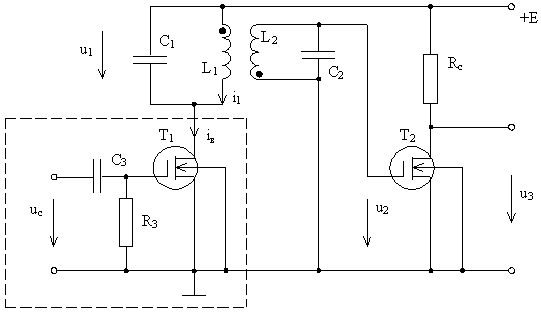 Рис. 5. Резонансный усилитель.
Рис. 5. Резонансный усилитель.
|
 Рис. 6. Эквивалентная схема резонансного усилителя.
Рис. 6. Эквивалентная схема резонансного усилителя.
|

Из этой системы по правилу Крамера найдём I 2, а затем по закону Ома для участка цепи найдём напряжение на конденсаторе С 2:
 ,
, 
или
 .
.
Введём проходное сопротивление:
 . .
| (1.12) |
Высший порядок уравнения равен удвоенному числу обобщённых переменных, т. е. удвоенному числу степеней свободы. Этот пример мы рассматривали операторным методом, который применим только к линейным системам.