Дужки Пуассона

Нехай рух системи описує рівняння Гамільтона: ,

а є одна із функцій механічного стану системи, наприклад імпульс, енергія. Візьмемо повну похідну по часу від функції

.

Перетворюючи користуючись рівнянням Гамільтона:

= .

Суму в попередній формулі позначаємо через [f, H]

Вона є диференціальним рівнянням оператором, який називається дужками Пуассона. В нових позначеннях для повної похідної функції f має формулу

.

Якщо функція є інтегралом руху

Якщо інтеграл не залежить від часу явно, то дужки Пуассона дорівнює нулю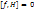

Дужки Пуассона можна скласти і для двох функцій дужки Пуассона антикомутативні .

Тільки для однакових функцій комутативні - . Дужки Пуассона мають властивість антисиметрії.

Дужки Пуассона взяті для самих канонічних змінних, називається фундаментальними дужками Пуассона:

За допомогою дужок Пуассона описуються інваріантні властивості системи, незалежні від вибору канонічних змінних. Фундаментальні дужки Пуассона мають квантово-механічний аналог – переставні відношення Гейзенберга.

46. Принцип екстремальної дії.
Дія. Принцип Гамільтона. Рівняння Лагранжа булиотриманіраніше з рівнянь Ньютона для системипов'язанихматеріальнихточок за допомогою принципу віртуальнихпереміщень та принципу Даламбера - Лагранжа. Однакрівняння Лагранжа можнаотримати з загального теоретичного принципу, що носить назвуваріаційного принципу екстремального (інодістаціонарного) дії. (Він же називається принципом Остроградського-Гамільтона.) Принципекстремальногодіїпоширенняречником не тільки на механічні, а й на квантово-механічним-етичнісистеми, поля, тому вінмаєнайважливішетеоретичнезначення.
Принцип екстремальногодіїможе бути застосований до складнихвиммеханічним системам зізв'язками. Однакрівняння для таких систем вжеотриманііззагальногорівняннямеханіки. Особливо важливо, що принцип екстремальногодіїзастосуємо для довільних систем у фундаментальнихсилових полях, а також для самих полів як систем з нескінченним числом ступенівсвободи. Зцієї причини принцип дозволяєотримуватифундаментальнірівнянняфізики як в механіці, так і за її межами.

Ми застосуємо принцип екстремальногодії для знаходженнярівняньрухувільної точки в потенційному і узагальнено-потенційномуполі.

Якщоповедінкасистемиописуєтьсяузагальненими Координатами (і деякими параметрами, такими, як маса, заряд) і відомафункція Лагранжа то можнаскластиінтегралдії:

Ця величина маєрозмірність «енергіячасу».

Зауважимо, що в попередніх параграфах описувалосянахождняфункції Лагранжа в процесі переходу віддекартовихкоорДіната до узагальнених за допомогоюрівняньзв'язку, понять узагальненоноїсили, кінетичноїенергії і потенційної. Зараз передвважаємо, щофункція Лагранжа задана.

Для визначення стану системи з s ступенями свободивибрано s узагальнених координат. Ввівшиконфігураційне простір s вимірів, можнарозглядатиузагальненікоординати Як яккоординати точки s вимірного простору. При русі система замінюєтьсяоднієїзображує точкою, щорухається в конфігураційномупросторі. Ця точка в просторіконфігураційописуєкриву, яку умовноможнаназватитраєкторієюрухусистеми.

Нехай маємо два станисистеми: у момент часу стан системивизначається точкою А простору конфігурацій, а в момент - точкою В. Принцип стаціонарноїдіїполягає в твердженні: з усіхрухів, які переводять системузі стану А в момент часу стан В у момент часу в дійсностіздійснюється те, для якогозвертається в нуль варіаціяінтеграладії:

Звернення в нуль варіаціїдії є необхідною умовоюйогоекстремуму. Цієюобставиною і пояснюєтьсяназва принципу.