Дискретные распределения вероятностей случайных величин

Большинство контрольных или испытательных процедур в теории надежности осуществляется в соответствии со схемой последовательных независимых испытаний Бернулли. Суть этой схемы сводится к следующему. Имеется N изделий, которые последовательно испытываются. Каждое такое испытание может завершиться одним из двух несовместных событий – некоторое событие А или наступает или не наступает. Например, изделие признается годным или бракуется. Обозначим вероятность наступления события А через р, тогда вероятность ненаступления этого события будет 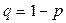. Если можно считать, что вероятность р не зависит от номера испытаний, то такая схема и носит название схемы последовательных независимых испытаний Бернулли.

Обозначим через x случайное событие заключающееся в появлении события А ровно k раз при N испытаниях. Можно доказать, что вероятность появления события А ровно k раз при N испытаниях определяется следующим соотношением:

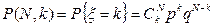, (32)

где 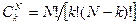– коэффициенты бинома Ньютона, 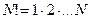– факториал числа N и 0! =1 – по определению.

ФРВ случайной величины x, отражающей появление события А не более k раз при N испытаниях, по определению (2) определяется соотношением:

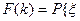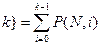< , (33)

Таблица 3 - Основные непрерывные распределения теории надежности

№	Название распределения	Область значений	Плотность распределения	Функция распределения вероятности	Математическое ожидание	Дисперсия
	Равномерное	(а, b)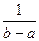
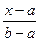
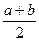
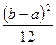
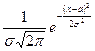
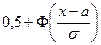
	Нормальное (Гаусса)	(-¥, ¥)			а	s 2
	Логарифмическое нормальное	(0, ¥)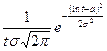
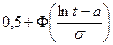
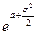
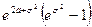
	Вейбулла	(0, ¥)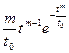
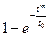
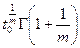
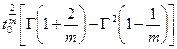
	Экспоненциальное	(0, ¥)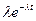
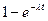
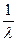
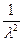
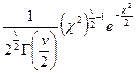
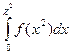
	c2-распределение	(0, ¥)			v	2v
	Стьюдента	(-¥, ¥)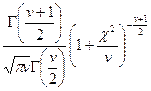

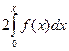
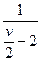
где 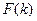– дает вероятность того, что событие А произойдет не более k раз.

Распределение случайной величины, описываемое соотношениями (32) или (33) носит название биномиального распределения.

Математическое ожидание и дисперсия этого распределения определяется соотношениями:

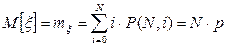, (34)

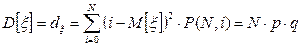. (35)

Часто при использовании схемы независимых последовательных испытаний Бернулли для большого числа испытываемых изделий вместо случайной величины x=k используют другую случайную величину 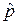, описывающую частость или частоту наступления события x,

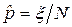. (36)

Оказывается, что частота 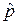наступления события А реализуется с той же вероятностью (32), что и число x событий А

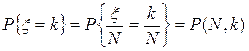. (37)

Поэтому ФРВ случайных величин x и 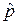имеют одинаковый вид (33), однако математическое ожидание и дисперсия для 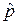имеют вид отличный от этих параметров для x:

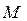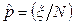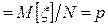[ ] , (38)

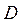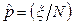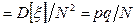[ ] . (39)

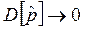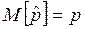В связи с тем, что , а при 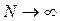, следует важное заключение о том, что частость наступления события является состоятельной, несмещенной и эффективной оценкой вероятности Р в последовательных независимых испытаниях Бернулли.

При использовании биномиального распределения в прикладных расчетах из-за сложности вычисления факториалов в (32) при больших N используют приближенные формулы.

Так, при р < 0, 1 и 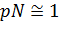используется расчет по распределению Пуассона

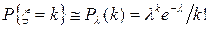, (40)

где .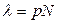

Есл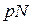и > 4 и 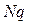> 4, то биномиальное распределение часто заменяют на нормальное с параметрам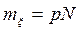и и 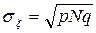(теорема Муавра-Лапласа):

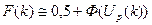, (41)

где .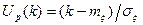

Кроме рассмотренных дискретных распределений в теории надежности также используются и некоторые другие распределения.