Моделирование сложных технических систем методом структурных схем

Сущность метода структурных схем заключается в том, что рассматриваемое изделие или система представляется в виде расчетной схемы, состоящей из отдельных элементов, которые в результате последовательного или параллельного их соединения образуют соответствующую структурную схему. Разбивка сложного изделия на отдельные элементы может быть произведена сколь угодно большим числом способов. Однако при этом необходимо соблюдать следующие принципы: 1. Каждый элемент должен выполнять вполне определенные функции и формировать определенный выходной параметр. 2. Каждый элемент должен иметь вполне определенные характеристики надежности. 3. Все элементы изделия могут иметь только по одному отказу. 4. Изделие представляется в виде единой структурной схемы, состоящей из суммы последовательных и параллельных соединений. События, изображенные в виде элементов и звеньев структурной схемы, должны быть независимы. 8. В структурной схеме не должно быть событий, среди которых одно событие является отрицанием другого. Одно и то же событие должно представляться в виде одного звена.

Основой структурных схем являются условные виды последовательных и параллельных соединений звеньев, выражающих событие безотказности действия отдельных элементов системы. Эти виды соединений не всегда совпадают с монтажными названиями соединений.

Последовательным соединением элементов с точки зрения надежности называется такое соединение, при котором для безотказной работы системы требуется безотказная работа всех элементов. Последовательное соединение графически представляют в виде рисунка 8, а.

Рисунок 8- Виды соединения элементов по надежности: а - последовательное соединение, б - параллельное соединение, в - смешанное соединение

Обозначим через Y _i случайное событие, заключающееся в безотказности работы i -элемента. Тогда событие Y_c, заключающееся в безотказности работы всей системы, наступит тогда и только тогда, когда наступят события Y ₁, Y ₂ ,..., Y_N. Используя независимость событий Y _i и то, что событие Y_c представимо в виде произведения исходных событий, получим для вероятности безотказной работы соотношение

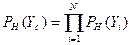или , (42)

где P_H(Y_c)=P_{H, C}, Р_H (Y_i)=Р_{H, i}.

Параллельным соединением элементов с точки зрения надежности называется такое соединение, при котором для безотказной работы системы требуется безотказная работа хотя бы одного элемента. Параллельное соединение графически представлено в виде рисунка 8, б.

Для установления связи между вероятностью безотказной работы системы и вероятностью безотказной работы элемента обозначим через Q_i случайное событие, заключающееся в отказе i -го элемента. Тогда для наступления отказа всей системы Q_c необходимо, чтобы отказали все элементы или наступило событие, равное произведению событий Q ₁, Q ₂,..., Q_N. Используя независимость событий Q_i и теорему умножения вероятностей, получим для вероятности наступления отказа и вероятности безотказной работы системы соотношения:

, . (43)

С помощью последовательного и параллельного соединения элементов можно смоделировать структурную схему для любой технической системы. Например, систему выпуска шасси некоторых самолетов можно представить в виде рисунка 8, в, где элемент 1 моделирует основную гидросистему, элементы 2 и 3 моделируют основную и аварийную системы выпуска шасси, а элемент 4 моделирует шасси. Обозначая вероятности безотказной работы каждого элемента через P_н (i), получим вероятность безотказной работы P_{н, с} для этой системы в виде .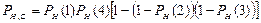

Рассмотрим расчетные формулы для вероятности безотказной работы и средней наработки до отказа сложной системы, состоящей из N элементов, в период её нормального функционирования.

Учитывая, что в период нормального функционирования вероятность безотказной работы i -ro элемента подчиняется экспоненциальному закону , получим для последовательного соединения:

. (44)

В случае l ₁ =l ₂ =...=l_N=l будем иметь , где m _{T, c}= m _T/ N, .

Из этих соотношений видно, что последовательное соединение элементов по надежности очень сильно снижает как вероятность безотказной работы системы, так и среднюю наработку до отказа. Например, система из 10 последовательных элементов в 10 раз уменьшит величину средней наработки до отказа, а вероятность безотказной работы системы за наработку t=m_T уменьшится почти в 10³ раз.

Для случая параллельного соединения N элементов с одинаковой интенсивностью отказов l получим:

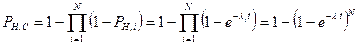. (45)

Из этого соотношения видно, что система параллельно соединенных элементов с экспоненциальными законами надежности не подчиняется экспоненциальному закону.

Средняя наработка до отказа такой системы определяется выражением:

. (46)

Из соотношений (45) и (46) видно, что параллельное соединение элементов по надежности увеличивает вероятность безотказной работы системы и среднюю наработку до отказа. Видно, что применение в системе параллельных элементов по надежности позволяет очень сильно повысить вероятность безотказной работы системы, однако средняя наработка до отказа с увеличением числа элементов возрастает существенно медленнее (43). Использование параллельного подключения элементов по надежности является одним из способов повышения показателей надежности сложных изделий резервированием.

Резервирование также используется в технологических системах производства. Так, если некоторый параметр качества детали подвергается контрольной процедуре, то важно считать, что эти два элемента (технологическая операция и контрольная процедура), с точки зрения надежности, включены параллельно.