Влияние качества технологической системы производства на выпуск бездефектной продукции

С позиции производства критерием выпуска бездефектной продукции является изготовление изделий, у которых все регламентированные в нормативно-технической документации значения показателей качества с заданной вероятность лежат в установленных допусках. Рассмотрим это положение с позиций теории надёжности.

Пусть в процессе стабильного производства некоторого изделия была взята выборка из N изделий, на которых замерено значение некоторого показателя качества X и получен следующий набор значений этого показателя x₁, x₂ , ...., x_N. При определённых условиях производства можно предполагать, что распределение показателя х подчиняется нормальному закону с математическим ожиданием m_П и стандартным отклонением . (Существует регламентированная процедура проверки этого утверждения). Тогда вероятность α того, что значение показателя x_i на некотором вновь изготовленном изделии лежит в интервале даётся следующим соотношением, вытекающим из (3) и (22):

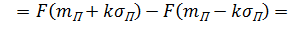
, (65)

где k =1, 2, 3… и использовано предположение, что .

Из соотношения (65) и таблицы 5 следует, что для достижения определённой уверенности в том, что значение показателя качества изделия лежит в заданном симметричном интервале с центром в точке математического ожидания необходимо величину этого интервала 2 выбирать достаточно большой, например, . В этом случае процент изделий, у которых значение показателя качества не попадает в этот интервал составит 0, 27%. Эти соображения формулируются, как правило «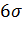», применяемое в технических стандартах многих стран и регламентирующие, в частности, величину допуска ∆ D= на отклонение параметра качества от среднего или номинального значения.

Таблица 5 - Вероятность попадания и непопадания γ значения параметра х в симметричный интервал 2 в зависимости от k

k
Размер интервала	2		6	8
	0, 68	0, 954	0, 9973	0, 999937
γ, %		4, 56	0, 27	0, 0064

Однако, как было показано ранее (п.5.3, 7.2, 7.3) величина этого допуска на рассеивание показателя качества изделия в значительной степени определяет вероятность безотказной работы изделия по этому показателю. Поэтому для обеспечения высокой вероятности безотказной работы изделия величина этого назначенного для производства допуска должна быть достаточно мала. Однако, с другой стороны уменьшение величины допуска ограничено возможностями реально используемой технологической системы производства, создающей рассеивание этого показателя с величиной стандартного отклонения . Использование же значений допусков, согласованных с возможностями реальной технологической системы изготовления изделия в рамках действующих стандартов, требует часто использования больших значений показателей запаса надёжности (см., например, (63) и таблицу 4) и, следовательно, приводит к снижению эффективности изделия за счёт увеличения его материалоёмкости. С другой стороны, использование же допусков существенно более жёстких по сравнению с возможностями используемой технологической системы производства ведёт к необходимости значительного увеличения контрольных и испытательных процедур и росту брака, что повышает стоимость и трудоёмкость производства.

Указанные соображения послужили основанием для многих развитых стран уже с 80-х годов прошлого столетия для перехода от стандартов, подчиняющихся правилу «6 », на стандарты, подчиняющиеся правилам «8 » и даже «10 ». Основная сложность перехода на более жёсткие стандарты связана с модернизацией технологической системы производства, требующей изготовления или закупки нового оборудования, технологической оснастки, средств измерения и контроля и т.д., удовлетворяющих этим новым более жёстким стандартам. Собственно именно в этом переходе лежит суть технологической революции, прошедшей в развитых странах в конце прошлого столетия. В бытовом плане результаты такой технологической революции наглядны при выпуске массовой продукции, когда в рамках стандартов «6 » и «8 » следует ожидать 0, 27% и 0, 0064% (таблица 5) брака, что при годовой программе, например, 10⁶ изделий даёт 2700 и 64 изделия, у которых следует ожидать отказ.

Вопрос о выполнении технологического задания производством можно рассмотреть и с более общих позиций. Пусть некоторый показатель качества, определяемый параметром X задан в конструкторской документации на изготовление своим номинальным значением m_Н и симметричным допуском ±∆ D на него. В процессе производства технологическая система обеспечивает получение значений этого показателя с распределением по нормальному закону с параметрами m_П и . Тогда вероятность выполнения технологического задания по этому параметру качества, определяемая как вероятность нахождения значения параметра X в интервале , вычисляется на основе соотношений, использованных при получении (65):

, (66)

где величина ε равная отклонению математического ожидания m_П от заданного его номинального значения m_Н даётся выражением:

. (67)

Используя регламентацию на отклонение значения параметра x_i от заданного номинального значения

(68)

и оценку математического ожидания m_П его средним значением получим:

(69)

Следовательно, значение параметра ε в зависимости от настройки технологической системы может изменяться в пределах (, ), приводя к изменению вероятности выполнения технологического задания (66) в пределах

, (70)

где максимальное значение достигается при и равно

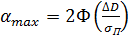, (71)

а минимальное значение определяется условием и равно

. (72)

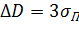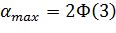Например, при выполнении технологического процесса в рамках стандарта «6 » с регламентацией точности изготовления условием (68) и получим, что вероятность выполнения технологического задания по рассмотренному параметру качества не менее 0, 5, но не более =0, 9972.

Следовательно, если при выполнении технологического процесса не проводится статистическая обработка результатов измерения x_i и не контролируется значение параметра ε (67), то для вновь изготовленного изделия можно только утверждать, что условие (68) выполняется с вероятностью не менее (72), а не с вероятностью =0, 9972, характеризующей стандарт «6 ». Для параметров качества, которые могут подвергаться сплошному оперативному контролю, не пропуск дефекта в этом случае определяется контрольной операцией.

Однако, обычно значение параметра меньше величины допуска и, более того, статистический контроль позволяет находить значение в долях допуска :

, 0≤ s< 1. (73)

Значение коэффициента s определяется по результатам регулярного выборочного контроля и, в зависимости от полученного значения, можно провести подналадку технологической системы для уменьшения его величины.

Используя (73) и придадим соотношению (66) следующий вид:

. (74)

В таблицы 6 на основе соотношения (74) приведены расчётные значения нижней и верхней границы вероятности выполнения технологического задания для различных случаев настройки по соотношению (73) технологических систем, удовлетворяющих стандартам «6 » и «8 ».

Таблица 6 - Нижняя и верхняя границы вероятности выполнения технологического задания по параметру качества для двух видов технологических систем в зависимости от их настройки по (73)

стандарт	«6 »	«8 »
k
s		0, 25	0, 5	0, 75			0, 25	0, 5	0, 75
	0, 9973	0, 987	0, 933	0, 77	0, 5	0, 99994	0, 9986	0, 977	0, 84	0, 5
	0, 9973	0, 99994

Из приведённых в таблице 6 данных видно, что при выполнении статистического контроля и настройки технологической системы по величине s (73) можно значительно повысить величину нижней оценки вероятности выполнения технологического задания и значительно уменьшить выпуск дефектной продукции. Так для рассмотренного выше примера при настройке технологической системы на s= 0, 75; 0, 5 или 0, 25 можно ожидать дефект в 13, 7 или только в 1 изделии из 100 изготовленных.

Особенно велика значимость статистического контроля и подналадки технологической системы по параметру s (73) при обеспечении высокой вероятности выполнения технологического задания по параметрам качества изделия, отнесённых ко второй группе (п.7.1), величину которых нельзя определить оперативно неразрушающим методом на изготовленном изделии. Действительно, в этом случае оценка вероятности выполнения технологического задания количественно может быть проведена только по данным предварительного выборочного контроля изделий с последующим исключением их из дальнейшего применения по назначению. Однако эти данные должны с определённой периодичностью подтверждаться для оценки возможного «дрейфа» среднего значения параметра качества в пределах оговорённых допусков, что как видно из табл.6 может значительно снижать вероятность выполнения технологического задания даже при строгом выполнении директивного технологического регламента. При этом, как следует из таблицы 5, даже использование технологических систем, удовлетворяющих более жестким стандартам, при значениях параметра s больших 0, 5 фактически полностью нивелируются их возможности по достижению высоких значений вероятности выполнения технологического задания.

Таким образом, проведённый анализ показывает, что для изготовления высоконадёжных летательных аппаратов с вероятностью безотказной работы 0, 999 и выше в течение назначенных ресурсов требуется высококачественные технологические системы производства, основанные на более жестких стандартах, чем существующие на многих заводах. При этом наличие таких технологических систем не является панацеей для выпуска бездефектной продукции. Необходим обязательный статистический постоянный или выборочный контроль, особенно за обоснованно регламентированными параметрами второй группы с обязательной подналадкой оборудования не только для нахождения параметра в оговоренном допуске, но и для минимизации отклонения среднего статистического его значения от заданной номинальной величины.