Оценка надежности выполнения задания технологической системой по параметрам качества продукции

Рассмотрим некоторый n -ый элемент технологической системы (рис. 12), который формирует параметры качества продукции х_i (n). Индекс i относится к i -ому показателю качества детали после выполнения технологической операции, соответствующей n -ому элементу.

Величина х_i зависит от свойств материала, режимов обработки, конструктивных особенностей обрабатывающей системы, точности настройки средств технологического оснащения, точности измерения самой величины и воздействия внешних факторов.

Свойства материала заготовки характеризуются не только средними значениями показателей качества, но и их рассеиванием, возникающим как в заготовках из одной плавки и партии, так и рассеиванием из-за наличия заготовок из разных плавок и разных партий.

Режимы обработки также характеризуются не только средними значениями, но и их рассеиванием из-за физико-химических флуктуации в зоне взаимодействия инструмента с деталью и наличия обратной связи в системе станок-приспособление-инструмент-деталь-приспособление-станок (система СПИД), а также рассеиванием из-за того, что система СПИД является нежесткой, теплопроводящей и т.д.

Точность настройки средств технологического оснащения и точность измерения параметра также характеризуются не только средними значениями, но и определенным рассеиванием, особенно в случае ручных операций.

Таким образом, любой параметр качества продукции х_i является сложной функцией переменных, которые являются случайными величинами, зависящими от наработки технологического элемента:

, (76)

где z_j - случайные величины, описывающие перечисленные выше факторы – показатели свойств материала, параметры режима обработки, параметры точности настройки средств технологического оснащения и т.д.

Для анализа влияния факторов z_j на показатель качества х_i необходимо знать в общем случае функции распределения случайных величин z_j. Однако с целью упрощения задачи воспользуемся соотношениями (п.8.3), считая, что величины z_j некоррелированы и характеризуются математическим ожиданием и стандартным отклонением . В этом случае параметр качества х_i в окрестности своего математического ожидания может быть описан (см. также (59) и (64)) распределением с параметрами:

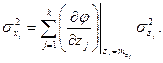(77)

Таким образом, соотношение (77) устанавливает приближенную связь между характеристиками распределения параметра качества продукции и характеристиками распределений показателей свойств заготовки и показателей технологической системы элемента.

Условием безотказности технологического элемента при выполнении задания (технологической операции) по параметру качества x_i за наработку Т будет выполнение неравенства:

, (78)

где x_{i, H} и x_{i, B} - нижнее и верхнее предельное отклонение для параметра x_i, установленное в нормативно-технической документации.

Вероятность выполнения задания n-ым технологическим элементом параметру x_i определяется из соотношения, аналогичного вероятности безотказной работы:

, (79)

где - вероятность события.

Естественно, эта вероятность является априорной, то есть вероятность до проведения контрольной операции определения значения параметра качества. После же проведения контрольной операции эта постаприорная вероятность при идеальной оперативной характеристике контроля (отсутствия погрешностей измерения) равна либо единице (параметр в допуске), либо нулю (параметр вне допуска).

Если задание технологической системы заключается в одновременном выполнении неравенства (78) для набора параметров от i =1 до i=k, то вероятность выполнения задания будет:

. (80)

В случае, когда величины x_i(t) независимы, соотношение (80) примет вид:

. (81)

При задании одностороннего допуска на параметр x_i в виде

или ,

соотношение (78) примет вид:

или ,

соответственно.

Вычисление вероятности P_i(n, t) производится по одному из алгоритмов, изложенных в п. 4, 5, 7.2-7.4.

Например, если известна плотность распределения f(x, t) параметра качества и заданы допуски х_Н и х_B на этот параметр в виде детерминированных величин, то вероятность выполнения задания будет равна:

. (82)

В случае, когда распределение f(x, t) определяется нормальным законом, выражение (82) примет вид:

, (83)

где - квантили нормального распределения; Ф(U_р) - интеграл ошибок, , , где - заданное номинальное значение параметра, и - заданные отклонения от номинального значения.

Этому соотношению (83) можно придать вид соотношения (66) и (74) и использовать анализ раздела 7.4 для повышения вероятности выполнения задания.

Таким образом, если известна плотность распределения вероятности параметра качества х, зависящая от параметров технологического элемента (76), и известны допуски х_B и х_H, то по соотношению (82) определяем вероятность выполнения задания технологической системой по этому параметру в течение заданной наработки как было сделано в п.7.4.

Если полученное значение P(n, t) меньше допустимого, то проводят анализ технологической системы и соответствующие мероприятия по повышению надежности технологической системы. Из (83) видно, что увеличить надежность P(n, t) можно в основном за счет уменьшения дисперсии s_х или, как следует из (77), за счет уменьшения дисперсии поставляемых заготовок, дисперсии режимов обработки и дисперсии средств технологического оснащения путем их подналадки или замены на более точные, либо за счёт подналадки системы для уменьшения параметра (п.7.4). Это второе направление реализуется существенно проще первого и только в случае не достижения нужного результата имеет смысл проводить более сложные мероприятия по первому направлению.

В процессе эксплуатации технологической системы параметры распределения т_х и s_х будут изменяться, приводя к изменению вероятности выполнения задания. Поэтому постоянный (или периодический) статистический контроль вероятности выполнения задания создает предпосылки для выпуска бездефектной продукции за счет оперативной подналадки технологической системы с целью восстановления её надежности и минимизации отклонения среднего статистического значения показателя качества от заданного его номинального значения. В этом случае возникает возможность выпускать бездефектную продукцию не за счет обнаружения уже полученного брака и последующей подналадки технологической системы, а за счет адаптивного управления качеством и изготовления бездефектной продукции.

На этапе технологической подготовки производства и проектирования технологической системы по заданным значениям P(n, t) и х_H и х_B осуществляют подбор составляющих технологической системы.

Отметим, что обратная задача определения допусков х_H и х_B по заданной величине P(n, t) не имеет в общем случае однозначного решения, так как соотношение (83) является одним уравнением с двумя неизвестными. В связи с этим задачу решают, либо выбирая допуски симметрично относительно т_х

, (84)

либо одна из границ допуска задается из конструктивных или технологических соображений, а другая - из решения уравнения (82) или (83).

Обычно в случае технологических допусков величину интервала [ х_B, х_H ]выбирают равной 6 s_х, что в случае симметричного интервала и нормального распределения часто считают соответствует вероятности выполнения задания P(n, t) = 0, 997, что в действительности неверно (п.7.4).

Для нахождения параметров распределения (82) и (83) конкретных технологических систем величина т_х и s_х выбирают либо из справочных данных, либо находят путем расчетов по данным специальных экспериментов, либо путем расчетов по данным, полученным в процессе эксплуатации этого элемента. До накопления большого статистического материала эти числовые характеристики можно оценить по предельным значениям х_тin и х_тax параметра, полученным при испытании технологической системы на основе соотношений:

,

где d - коэффициент, зависящий от числа испытаний N (таблица 7).

Таблица 7 - Зависимость коэффициента d от числа испытаний N

Если параметр качества x_j, формируемый i -ым технологическим элементом с вероятностью , подвергается контрольной процедуре с вероятностью обнаружения дефекта P ^(к), то эти два элемента (технологическая операция и операция контроля) с точки зрения надежности имеют параллельное включение (рисунок 14).

Вероятность выполнения задания технологической системой увеличивается за счет введения контрольной операции и определяется соотношением:

, (88)

где - риск потребителя.

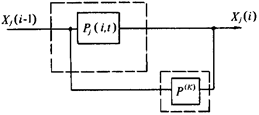
Рисунок 14 - Структурная схема расчета надежности при включении операции контроля j-го параметра качества в технологическую систему

Контрольные вопросы к разделу 7

1. Структурная схема взаимосвязи параметров технологического процесса с показателями надежности изделий.

2. Соотношение для определения вероятности безотказной работы изделия для случая, когда эксплуатационный показатель качества изделия и его допустимое предельное значение, определяемое внешними воздействиями, распределены по нормальному закону. Коэффициент запаса надежности и коэффициенты вариации эксплуатационного показателя качества и его допустимого предельного значения.

3. По каким причинам снижение значений коэффициентов вариации параметра качества и его допустимого предельного значения более эффективно, чем увеличение коэффициента запаса надёжности?

4. Зависимость коэффициента вариации эксплуатационного показателя качества от коэффициентов вариации показателей качества деталей при выполнении технологических операций изготовления изделия?

5. Влияние качества технологической системы производства на выпуск бездефектной продукции. Понятие о стандартах «6σ» и вероятность выпуска бездефектной продукции в рамках этих стандартов.

6. Основные причины отказов, связанные с технологией изготовления изделий?

7. Причины недостаточной обоснованности технических условий на изготовление изделий?

8. Чем определяется недостаточная надежность технологических систем изготовления изделий?

9. Остаточные и побочные явления в изделиях при выполнении технологических операций их изготовления?

10. Понятие о долговечности материала в рамках кинетической прочности и суммировании парциальных повреждений при выполнении технологического процесса и эксплуатации изделий.

11. Основные мероприятия повышения надежности изделий на этапе производства.

12. Понятие о технологической системе производства и вероятности выполнения технологического задания.

13. Оценка вероятности выполнения задания технологической системой по параметрам качества продукции.

14. Понятие о контрольной операции как о резервировании технологической системы.