
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы содержания, проверяемые заданиями КИМ
|
|
Описание проекта экзаменационной модели для проведения
Единого государственного экзамена по МАТЕМАТИКЕ углубленного уровня
В соответствии с требованиями ФГОС среднего (полного) общего образования
ПРОЕКТ
I. Кодификаторы для создания экзаменационной модели по математике базового уровня для государственной итоговой аттестации обучающихся, освоивших основные общеобразовательные программы среднего (полного) общего образования
Кодификатор подготовлен в соответствии с предметными требованиями по математике Федерального государственного образовательного стандарта среднего (полного) общего образования (Приказ Министерства образования и науки РФ от 17 мая 2012 г. №413) и с учетом содержания наиболее востребованных предметных программ для ступени среднего (полного) общего образования, которые рекомендованы к использованию в образовательных организациях в условиях введения ФГОС и содержания учебно-методических комплектов, рекомендованных к использованию в образовательных организациях в условиях введения ФГОС.
Кодификатор 1 содержат планируемые результаты обучения (ПРО), которые детализируют предметные требования ФГОС СОО и операционализованные умения (ОУ), которые являются объектом контроля в рамках государственной итоговой аттестации за курс средней школы.
Кодификатор 2 включает перечень элементов содержания (ЭС), на базе которых разрабатываются задания для оценки достижения планируемых результатов обучения.
Раздел 1. Планируемые результаты обучения и операционализированные умения
В первом столбце указан код планируемого результата обучения, во втором столбце – код операционализированного умения.
| Код раздела | Код ОУ | Планируемые результаты обучения (ПРО), операционализированные умения (ОУ) |
| Элементы теории множеств и логики | ||
| 1.1 | Оперировать на базовом уровне[1] понятиями: конечное множество, элемент множества, подмножество, пересечение и объединение множеств, числовые множества на координатной прямой, отрезок, интервал; находить пересечение и объединение двух множеств на числовой прямой; строить на числовой прямой подмножество числового множества, заданное простейшими условиями | |
| 1.2 | Оперировать на базовом уровне понятиями: утверждение, отрицание, истинные и ложные утверждения, причина, следствие, частный случай общего утверждения; распознавать ложные утверждения, ошибки в рассуждениях; уметь строить контрпримеры в несложных случаях | |
| 1.3 | Использовать числовые множества на координатной прямой для описания реальных процессов и явлений; проводить логические рассуждения в ситуациях повседневной жизни | |
| Числа и выражения | ||
| 2.1 | Оперировать на базовом уровне понятиями: целое число, делимость чисел, обыкновенная дробь, десятичная дробь, рациональное число, иррациональное число, действительное число, приближённое значение, часть, доля, отношение, процент, повышение и понижение на заданное число процентов, масштаб; выполнять арифметические действия; сравнивать числа между собой; изображать числа точками на числовой прямой; вычислять значения выражений с помощью преобразований и подстановок | |
| 2.2 | Выполнять несложные преобразования целых и дробно-рациональных выражений; выражать в простейших случаях из равенства одну переменную через другие | |
| 2.3 | Выполнять несложные преобразования выражений, содержащих степени, корни, логарифмы; оценивать и сравнивать целые степени чисел, корни, логарифмы в простых случаях; изображать на числовой прямой целые степени, корни, логарифмы чисел в простых случаях | |
| 2.4 | Оперировать на базовом уровне понятиями: тригонометрическая окружность, величина угла, градусная мера угла, заданного точкой на окружности, синус, косинус, тангенс и котангенс; изображать схематически углы данной величины; определять знаки синуса, косинуса, тангенса, котангенса | |
| 2.5 | При решении практических задач выполнять расчёты (при необходимости – с использованием справочных материалов и вычислительных устройств); соотносить реальные величины с их числовыми значениями; использовать округление, приближения и прикидки при решении повседневных задач | |
| Уравнения и неравенства | ||
| 3.1 | Решать линейные уравнения и неравенства, квадратные уравнения и неравенства | |
| 3.2 | Решать простейшие показательные уравнения и неравенства | |
| 3.3 | Решать простейшие логарифмические уравнения и неравенства | |
| 3.4 | Уметь приводить примеры аргументов тригонометрических функций, имеющих табличные значения | |
| 3.5 | Пользоваться алгебраическими методами при решении несложных практических задач | |
| Функции | ||
| 4.1 | Оперировать на базовом уровне понятиями: зависимость, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание и убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, периодическая функция, период | |
| 4.2 | Определять по графику функции: приближённые значения, нули, промежутки знакопостоянства, монотонности, наибольшие и наименьшие значения, точки экстремума, период, элементы симметрии графика | |
| 4.3 | Оперировать на базовом уровне понятиями: прямая и обратная пропорциональность, линейная, квадратичная, логарифмическая и показательная функции, тригонометрические функции; распознавать графики этих функций и соотносить их с формулами | |
| 4.4 | Строить эскиз графика функции по известным свойствам (промежутки возрастания/убывания, значение функции в заданной точке, точки экстремумов, и т.д.) | |
| 4.5 | Определять по графикам свойства реальных процессов и зависимостей; интерпретировать свойства в контексте конкретной практической ситуации | |
| Элементы математического анализа | ||
| 5.1 | Оперировать на базовом уровне понятиями: производная функция, значение производной в точке, касательная к графику функции; иметь представление о геометрическом и физическом смысле производной; определять значение производной функции в точке по изображению касательной к графику | |
| 5.2 | Вычислять табличные производные элементарных функций; использовать производную при решении несложных задач на исследование функций | |
| 5.3 | Оценивать скорость изменения величины или процесса в разные моменты времени, пользуясь графиками реальных зависимостей; сравнивать скорости процессов по графикам | |
| Статистика и теория вероятностей | ||
| 6.1 | Владеть на базовом уровне методами табличного и графического представления данных | |
| 6.2 | Оперировать на базовом уровне понятиями: числовой набор, среднее значение; уметь находить описательные характеристики (среднее арифметическое, медиану, наибольшее и наименьшее значения, размах, дисперсию и стандартное отклонение) наборов числовых данных | |
| 6.3 | Оперировать на базовом уровне понятиями: случайный эксперимент, элементарное событие, случайное событие, вероятность случайного события, невозможное и маловероятное событие, достоверное событие; вычислять вероятности событий в опытах с равновозможными исходами в простейших случаях | |
| 6.4 | Оценивать и сравнивать в простых случаях вероятности событий повседневной жизни; читать, сопоставлять, сравнивать, интерпретировать в простых случаях реальные данные, представленные в виде таблиц, диаграмм, графиков; понимать смысл закона больших чисел и его роль в социологии, страховании, здравоохранении, обеспечении безопасности населения в чрезвычайных ситуациях | |
| Текстовые задачи | ||
| 7.1 | Решать несложные текстовые задачи; анализировать условие, при необходимости составлять по условию уравнения или системы уравнений; действовать по алгоритму, описанному в условии; использовать рассуждения; выбирать данные, необходимые для решения задачи; осуществлять несложный перебор вариантов, выбирая наилучший; анализировать и интерпретировать решения в контексте условия задачи | |
| 7.2 | Решать задачи на расчёт стоимости покупок, услуг и т.п.; на проценты (скидки, наценки) и на вычисление сложных процентов в несложных случаях (вклады, кредиты и т.п.); решать повседневные задачи, связанные с переводом одних единиц в другие (в частности, единиц температуры, длины, массы, времени; уметь пользоваться масштабом на картах, планах помещений, выкройках, при работе на компьютере и т.п. | |
| Геометрия | ||
| 8.1 | Владеть на базовом уровне понятиями о плоских фигурах, их свойствах, решать несложные планиметрические задачи с использованием изученных фактов и теорем планиметрии | |
| 8.2 | Оперировать на базовом уровне понятиями: точка, прямая, плоскость в пространстве, параллельность и перпендикулярность прямых и плоскостей; изображать изучаемые фигуры; делать (выносные) плоские чертежи из рисунков фигур; извлекать из чертежей и рисунков информацию о пространственных фигурах | |
| 8.3 | Решать несложные задачи на взаимное расположение прямых и плоскостей в пространстве с использованием фактов стереометрии | |
| 8.4 | Распознавать простые многогранники (призма, пирамида, прямоугольный параллелепипед, куб) и пользоваться их свойствами для решения простых задач; уметь находить их элементы, пользуясь стереометрическими фактами и свойствами фигур | |
| 8.5 | Распознавать тела вращения (конус, цилиндр, сфера и шар) и пользоваться их свойствами для решения простых задач; уметь находить их элементы, пользуясь стереометрическими фактами и свойствами фигур | |
| 8.6 | Пользоваться на базовом уровне прямоугольной системой координат в пространстве | |
| 8.7 | Соотносить абстрактные геометрические фигуры с физическими объектами; использовать свойства фигур для решения задач практического содержания; соотносить площади поверхностей тел одинаковой формы различного размера; соотносить объемы сосудов одинаковой формы различного размера | |
| История математики | ||
| 9.1 | Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки; знать примеры математических открытий и их авторов в связи с отечественной и всемирной историей; понимать роль математики в развитии цивилизации | |
| Методы математики | ||
| 10.1 | Применять известные методы при решении стандартных математических задач; замечать и характеризовать математические закономерности в окружающей действительности |
Элементы содержания, проверяемые заданиями КИМ
В первом и втором столбцах таблицы указываются коды содержательных блоков, на которые разбит учебный курс. В первом столбце жирным шрифтом обозначены коды разделов (крупных содержательных блоков), во втором столбце – коды тем. В третьем столбце указывается код элемента содержания (ЭС), на базе которых разрабатываются задания для оценки достижения планируемых результатов обучения.
| Код раздела | Код ЭС | Элементы содержания, проверяемые заданиями КИМ |
| Элементы теории множеств и логики | ||
| 1.1 | Множество, элемент множества, подмножество, пересечение, объединение, разность множеств, числовые множества, числовые промежутки | |
| 1.2 | Утверждение, отрицание, истинные и ложные утверждения, утверждение-следствие, контрпримеры, дизъюнкция, конъюнкция | |
| Числа и выражения | ||
| 2.1 | Натуральные числа, целые числа, обыкновенные дроби, десятичные дроби, рациональные числа, иррациональные числа, действительные числа, арифметические действия с числами | |
| 2.2 | Позиционная система счисления. Десятичная система счисления, двоичная система счисления, римские цифры | |
| 2.3 | Признаки делимости на 2, 3, 4, 5, 8, 6, 9, 10, 11. Делимость суммы и произведения целых, деление с остатком, НОД и НОК | |
| 2.4 | Степень с целым, рациональным и действительным показателем; корни; логарифм числа; синус, косинус, тангенс и котангенс числа | |
| Уравнения и неравенства | ||
| 3.1 | Уравнение с одной переменной. Корень уравнения. Система уравнений с двумя переменными. Решение системы. Линейные уравнения; квадратные уравнения. Целые уравнения более высоких степеней; дробно-рациональные уравнения. Равносильность уравнений, неравенств и их систем | |
| 3.2 | Теорема Виета для квадратного уравнения. Теорема Виета для уравнения степени 3 и выше. Теорема Безу | |
| 3.3 | Иррациональные уравнения | |
| 3.4 | Показательные и логарифмические уравнения | |
| 3.5 | Арксинус, арккосинус и арктангенс числа. Тригонометрические уравнения | |
| 3.6 | Неравенство с одной переменной. Решение неравенства. Линейные и квадратные неравенства. Дробно-рациональные неравенства | |
| 3.7 | Показательные и логарифмические неравенства | |
| 3.8 | Графическая интерпретация уравнений, неравенств и их систем двух переменных на плоскости | |
| 3.9 | Решение уравнений в целых числах | |
| Функции | ||
| 4.1 | Функция, аргумент и значение функции, область определения и множество значений функции, график функции, нули функции, промежутки знакопостоянства, возрастание и убывание, наибольшее и наименьшее значение, точки экстремума, непрерывность, точка разрыва, периодичность, четность и нечетность функций | |
| 4.2 | Обратная функция и ее график | |
| 4.3 | Линейная функция, ее свойства и график. Угловой коэффициент прямой. Квадратичная функция, ее свойства и график. Обратная пропорциональность, ее свойства и график | |
| 4.4 | Степенная функция, ее свойства и график. Функция 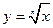
| |
| 4.5 | Показательная функция, ее свойства и график | |
| 4.6 | Логарифмическая функция, ее свойства и график | |
| 4.7 | Тригонометрические функции, их свойства и график. Обратные тригонометрические функции, их свойства и графики | |
| 4.8 | Преобразования графиков функций. Графики функций  , , 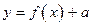 , , 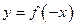 , , 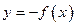 , , 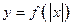 , , 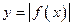 . График кусочно заданной функции . График кусочно заданной функции
| |
| 4.9 | Числовая последовательность. Арифметическая прогрессия, ее свойства. Формула общего члена, формула суммы. Геометрическая прогрессия, ее свойства. Формула общего члена, формула суммы первых членов. Сходящаяся геометрическая прогрессия, формула суммы сходящейся геометрической прогрессии | |
| Элементы математического анализа | ||
| 5.1 | Производная, геометрический смысл производной, физический смысл производной. Дифференцируемые функции. Угловой коэффициент касательной к графику функции. Скорость материальной точки | |
| 5.2 | Правила дифференцирования. Производные элементарных функций | |
| 5.3 | Применение производной при исследовании элементарных функций, нахождение точек экстремума, наибольших и наименьших значений функций, при построении графиков | |
| 5.4 | Первообразная функции, площадь криволинейной трапеции, определенный интеграл, формула Ньютона-Лейбница | |
| Статистика и теория вероятностей | ||
| 6.1 | Табличное и графическое представление данных. Числовые наборы; среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия и стандартное отклонение, генеральная совокупность, выборка | |
| 6.2 | Случайный эксперимент, элементарное событие, случайное событие, вероятность случайного события; формула сложения вероятностей. Случайный выбор. Вероятности событий в опытах с равновозможными элементарными событиями | |
| 6.3 | Независимые события. Вероятность пересечения независимых событий. Условная вероятность. Формула полной вероятности | |
| 6.4 | Испытание Бернулли. Вероятность числа успехов в серии испытаний Бернулли | |
| 6.5 | Дискретная случайная величина. Распределение вероятностей. Математическое ожидание, дисперсия и стандартное отклонение случайной величины. Математическое ожидание и дисперсия случайной величины «Число успехов». Математическое ожидание и дисперсия частоты события. Закон больших чисел | |
| 6.6 | Непрерывная случайная величина. Плотность вероятности. Важные непрерывные распределения: равномерные показательное, нормальное | |
| Текстовые задачи | ||
| 7.1 | Решение текстовых задач на движение, совместную работу, проценты, доли и части | |
| 7.2 | Решение задач с помощью организованного перебора вариантов | |
| Геометрия | ||
| 8.1 | Фигуры на плоскости, их свойства; теоремы планиметрии | |
| 8.2 | Взаимное расположение прямых и плоскостей в пространстве. Теоремы о взаимном расположении прямых и плоскостей. Проекция фигуры на плоскость. Теорема о трех перпендикулярах | |
| 8.3 | Углы в пространстве между прямыми и плоскостями. Трехгранный и многогранный угол | |
| 8.4 | Многогранники: призма, параллелепипед, тетраэдр, пирамида. Их элементы. Построение сечений Прямоугольный параллелепипед. Теорема Пифагора в пространстве | |
| 8.5 | Тела вращения: цилиндр, конус, шар и сфера, их элементы. Сечения тел вращения | |
| 8.6 | Теорема Эйлера. Пять видов правильных многогранников | |
| 8.7 | Вычисление элементов пространственных тел (длины ребер, углы). Вычисление площадей поверхностей и объемов многогранников и тел вращения | |
| 8.8 | Касательная прямая и плоскость. Теоремы о касательных в пространстве. Вписанные и описанные сферы | |
| 8.9 | Подобные тела в пространстве. Соотношения между площадями поверхностей и объемами подобных фигур | |
| 8.10 | Система координат в пространстве. Координаты точки. Вектор. Координаты вектора | |
| 8.11 | Коллинеарные и компланарные векторы. Сложение векторов. Умножение вектора на число, скалярное произведение векторов. Вычисление длин и углов с помощью векторов | |
| 8.12 | Уравнение плоскости, уравнения прямой в пространстве, уравнение сферы, формула расстояния между точками |
ПРОЕКТ