
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Система оценивания
|
|
Ответы к заданиям 1–9
Каждое из заданий 1–9 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается
1 баллом.
| № задания | Ответ |
| 3, 3 | |
| 0, 6 | |
| 178; 187; 718; 781; 817; 871 | |
| –5 |
Решения и критерии оценивания заданий 10–16
Количество баллов, выставляемых за выполнение заданий 10–16, зависит от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, в частности все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.
В критериях оценивания конкретных заданий содержатся общие требования к выставлению баллов.
При выполнении задания можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.
| 10 |
а) Решите уравнение 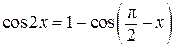 .
.
б) Найдите все корни этого уравнения, принадлежащие промежутку  .
.
Решение. а) Преобразуем обе части уравнения:
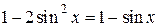 ;
;  ;
;  ,
,
откуда  или
или 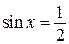 .
.
Из уравнения  находим:
находим:  , где
, где 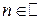 .
.
 Из уравнения
Из уравнения 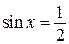 находим:
находим:  , где
, где 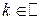 .
.
б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку  .
.
Получаем числа:  ;
;  ;
;  .
.
Ответ: а) 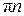 ,
, 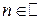 ;
;  ,
, 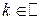 .
.
б)  ;
;  ;
;  .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а или пункте б ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| 11 |
Все рёбра правильной треугольной призмы 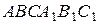 имеют длину
имеют длину 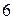 . Точки
. Точки 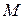 и
и 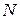 — середины рёбер
— середины рёбер  и
и 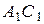 соответственно.
соответственно.
а) Докажите, что прямые 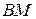 и
и 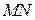 перпендикулярны.
перпендикулярны.
б) Найдите угол между плоскостями  и
и  .
.

|
Решение. а) Пусть точка 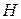 — середина
— середина 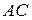 . Тогда
. Тогда
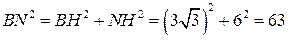 .
.
С другой стороны,
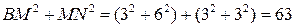 ,
,
а тогда по теореме, обратной теореме Пифагора, треугольник  является прямоугольным с прямым углом
является прямоугольным с прямым углом 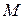 .
.
б) Проведём перпендикуляр  к прямой
к прямой  . Тогда
. Тогда  и
и  . Следовательно,
. Следовательно,  . Поэтому
. Поэтому  — проекция
— проекция 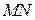 на плоскость
на плоскость  .
.
Прямая 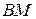 перпендикулярна
перпендикулярна 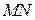 , тогда по теореме о трёх перпендикулярах
, тогда по теореме о трёх перпендикулярах  . Следовательно, угол
. Следовательно, угол  — линейный угол искомого угла.
— линейный угол искомого угла.
Длина  равна половине высоты треугольника
равна половине высоты треугольника  , то есть
, то есть 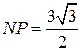 . Поэтому
. Поэтому  .
.
Следовательно,  .
.
Ответ: б) 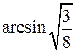 .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в пунктах а и б | |
| Выполнен только один из пунктов а и б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| 12 |
Решите неравенство  .
.
Решение. Левая часть неравенства определена при 
При  получаем
получаем  ,
, 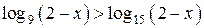 , поэтому левая часть неравенства отрицательна и не превосходит
, поэтому левая часть неравенства отрицательна и не превосходит 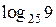 .
.
При  получаем
получаем  ,
, 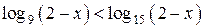 , поэтому левая часть неравенства отрицательна и не превосходит
, поэтому левая часть неравенства отрицательна и не превосходит 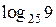 .
.
Таким образом, решение исходного неравенства  и
и 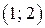 .
.
Ответ: 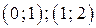 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Допущена единичная вычислительная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| 13 |
Две окружности касаются внешним образом в точке 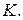 Прямая
Прямая 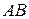 касается первой окружности в точке
касается первой окружности в точке  , а второй — в точке
, а второй — в точке 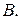 Прямая
Прямая 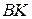 пересекает первую окружность в точке
пересекает первую окружность в точке  прямая
прямая 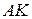 пересекает вторую окружность в точке
пересекает вторую окружность в точке 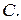
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника 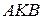 , если известно, что радиусы окружностей равны 4 и 1.
, если известно, что радиусы окружностей равны 4 и 1.

Решение. а) Обозначим центры окружностей  и
и 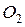 соответственно. Пусть общая касательная, проведённая к окружностям в точке
соответственно. Пусть общая касательная, проведённая к окружностям в точке 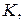 пересекает
пересекает 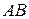 в точке
в точке  По свойству касательных, проведённых из одной точки,
По свойству касательных, проведённых из одной точки,  и
и  Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.
Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.
Вписанный угол  прямой, поэтому он опирается на диаметр
прямой, поэтому он опирается на диаметр 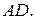 Значит,
Значит, 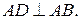 Аналогично, получаем, что
Аналогично, получаем, что 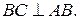 Следовательно, прямые AD и BC параллельны.
Следовательно, прямые AD и BC параллельны.
б) Пусть, для определённости, первая окружность имеет радиус 4,
а вторая — радиус 1.
Треугольники  и
и  подобны,
подобны, 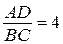 . Пусть
. Пусть 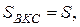 тогда
тогда 
У треугольников AKD и AKB общая высота, следовательно,  то есть
то есть 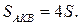 Аналогично,
Аналогично,  Площадь трапеции
Площадь трапеции  равна
равна  .
.
Вычислим площадь трапеции ABCD. Проведём к  перпендикуляр
перпендикуляр  равный высоте трапеции, и найдём его из прямоугольного треугольника
равный высоте трапеции, и найдём его из прямоугольного треугольника  :
:
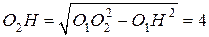 .
.
Тогда
 .
.
Следовательно, 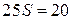 , откуда
, откуда  и
и 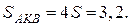
Ответ: 3, 2.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а, и обоснованно получен верный ответ в пункте б | |
| Получен обоснованный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
31 декабря 2013 года Сергей взял в банке  рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение. Пусть сумма кредита равна 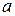 , ежегодный платеж равен
, ежегодный платеж равен 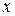 рублей, а годовые составляют
рублей, а годовые составляют  %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент
%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент  После первой выплаты сумма долга составит:
После первой выплаты сумма долга составит: 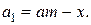 После второй выплаты сумма долга составит:
После второй выплаты сумма долга составит:

После третьей выплаты сумма оставшегося долга:
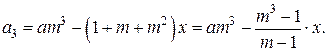
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому  , откуда
, откуда  .
.
При  и
и  получаем:
получаем:  и
и
 (рублей).
(рублей).
Ответ: 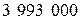 рублей.
рублей.
| Содержание критерия | Баллы |
| Обоснованно получен правильный ответ | |
| Получено верное выражение для ежегодного платежа, но допущена вычислительная ошибка, приведшая к неверному ответу | |
| С помощью верных рассуждений получено уравнение, из которого может быть найдено значение ежегодного платежа, но коэффициенты уравнение неверные из-за ошибки в вычислениях | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| 15 |
Найдите все положительные значения 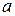 , при каждом из которых система
, при каждом из которых система
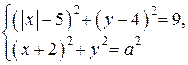
имеет единственное решение.
Решение. Если  , то уравнение
, то уравнение 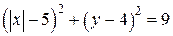 задаёт окружность
задаёт окружность 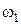 с центром в точке
с центром в точке  радиуса
радиуса 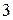 , а если
, а если  , то оно задаёт окружность
, то оно задаёт окружность  с центром в точке
с центром в точке  того же радиуса (см. рис.).
того же радиуса (см. рис.).
При положительных значениях 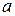 уравнение
уравнение  задаёт окружность
задаёт окружность  с центром в точке
с центром в точке 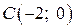 радиуса
радиуса 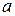 . Поэтому задача состоит в том, чтобы найти все значения
. Поэтому задача состоит в том, чтобы найти все значения 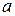 , при каждом из которых окружность
, при каждом из которых окружность  имеет единственную общую точку с объединением окружностей
имеет единственную общую точку с объединением окружностей  и
и  .
.
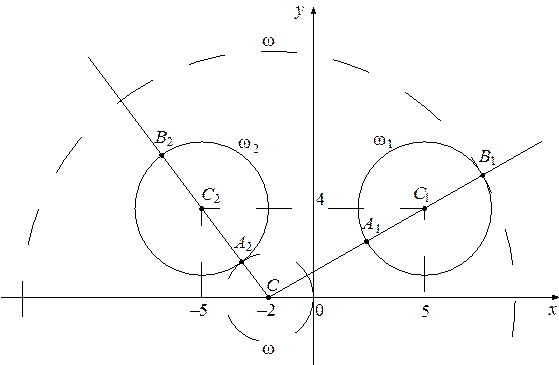
Из точки  проведём луч
проведём луч  и обозначим через
и обозначим через  и
и  точки его пересечения с окружностью
точки его пересечения с окружностью  , где
, где 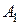 лежит между
лежит между  и
и  . Так как
. Так как 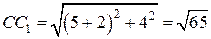 , то
, то 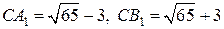 .
.
При  или
или  окружности
окружности  и
и 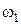 не пересекаются.
не пересекаются.
При 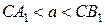 окружности
окружности 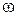 и
и  имеют две общие точки.
имеют две общие точки.
При 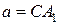 или
или  окружности
окружности 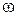 и
и 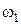 касаются.
касаются.
Из точки  проведём луч
проведём луч 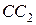 и обозначим через
и обозначим через  и
и 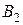 точки его пересечения с окружностью
точки его пересечения с окружностью  , где
, где  лежит между
лежит между  и
и  . Так как
. Так как 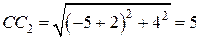 , то
, то  .
.
При  или
или 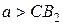 окружности
окружности 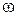 и
и  не пересекаются.
не пересекаются.
При  окружности
окружности 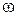 и
и  имеют две общие точки.
имеют две общие точки.
При 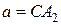 или
или 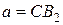 окружности
окружности 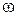 и
и  касаются.
касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность 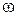 касается ровно одной из двух окружностей
касается ровно одной из двух окружностей 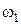 и
и  и не пересекается с другой. Так как
и не пересекается с другой. Так как 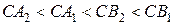 , то условию задачи удовлетворяют только числа
, то условию задачи удовлетворяют только числа  и
и 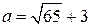 .
.
Ответ:  .
.
-
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано | |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра | |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| 16 |
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 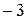 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно
, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 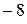 .
.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение. Пусть среди написанных чисел 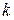 положительных,
положительных, 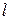 отрицательных и
отрицательных и  нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому
нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому 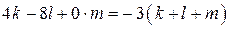 .
.
а) Заметим, что в левой части приведённого выше равенства каждое слагаемое делится на 4, поэтому  — количество целых чисел — делится на 4. По условию
— количество целых чисел — делится на 4. По условию 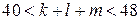 , поэтому
, поэтому  Таким образом, написано 44 числа.
Таким образом, написано 44 числа.
б) Приведём равенство  к виду
к виду  . Так как
. Так как 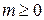 , получаем, что
, получаем, что  , откуда
, откуда 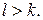 Следовательно, отрицательных чисел больше, чем положительных.
Следовательно, отрицательных чисел больше, чем положительных.
в) Подставим 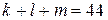 в правую часть равенства
в правую часть равенства  :
:  , откуда
, откуда 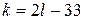 . Так как
. Так как 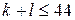 , получаем:
, получаем: 


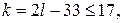 то есть положительных чисел не более 17.
то есть положительных чисел не более 17.
Приведём пример, когда положительных чисел ровно 17. Пусть на доске 17 раз написано число 4, 25 раз написано число 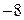 и два раза написан 0. Тогда
и два раза написан 0. Тогда  ; указанный набор удовлетворяет всем условиям задачи.
; указанный набор удовлетворяет всем условиям задачи.
Ответ: а) 44; б) отрицательных; в) 17.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: — обоснованное решение пункта а; — обоснованное решение пункта б; — искомая оценка в пункте в; — в пункте в приведёнпример, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
В соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам среднего общего образования (приказ Минобрнауки России от 26.12.2013 г. №1400 зарегистрирован Минюстом России 03.02.2014 г. № 31205),
«61. По результатам первой и второй проверок эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы ЕГЭ с развёрнутым ответом...»;
«62. В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.
Эксперту, осуществляющему третью проверку, предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу».
1. 1) Работа участника ЕГЭ направляется на третью проверку, если расхождение в баллах, выставленных двумя экспертами за выполнение любого из заданий, составляет 2 и более баллов.
В этом случае третий эксперт проверяет только ответ на то задание, которое было оценено двумя экспертами со столь существенным расхождением.
2. 2) Работа участника ЕГЭ направляется на третью проверку, при наличии расхождений хотя бы в двух заданиях.
В этом случае третий эксперт перепроверяет ответы на все задания работы.
[1] Здесь и далее – распознавать конкретные примеры общих понятий по характерным признакам, выполнять действия в соответствии с определением и простейшими свойствами понятий, конкретизировать примерами общие понятия.