Кинематика. Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.

Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения надо выбрать систему отсчета.

Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

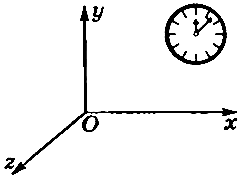
Рис. 1

Положение тела можно определить с помощью радиуса-вектора 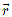или с помощью координат.

Радиус-вектор 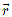точки — направленный отрезок прямой, соединяющий начало отсчета О с точкой (рис. 2).

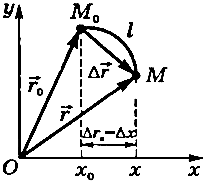
Рис. 2

Координата x точки — это проекция конца радиуса-вектора точки на ось Ох. Обычно пользуются прямоугольной системой координат. В этом случае положение точки на линии, плоскости и в пространстве определяют соответственно одним (x), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).

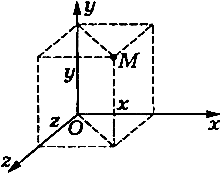
Рис. 3

В элементарном курсе физики изучают кинематику движения материальной точки.

В дальнейшем под словом " тело" будем понимать " материальная точка".

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.

Перемещение 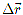тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка 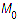) и конечное (точка М) положение тела (см. рис. 2):

,

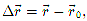где 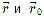— радиусы-векторы тела в эти моменты времени.

Проекция перемещения на ось Ox

,

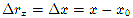где 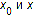— координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути .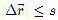

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

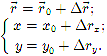
Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Средняя скорость 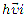— векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):

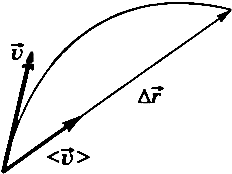
Рис. 4

В СИ единицей скорости является метр в секунду (м/с).

Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.

Иногда пользуются средней скоростью пути

,

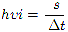где s — путь, пройденный за промежуток времени 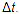. Средняя скорость пути — это скалярная величина.

Мгновенная скорость 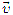тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени 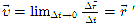. Здесь 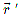— производная от радиуса-вектора по времени.

В проекции на ось Ох:

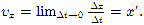
Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:

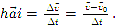
Вектор 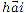направлен параллельно вектору изменения скорости 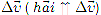в сторону вогнутости траектории (рис. 5).

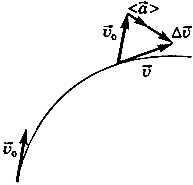
Рис. 5

Мгновенное ускорение:

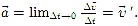
В СИ единицей ускорения является метр на секунду в квадрате (м/с2).

В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.

При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы 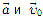сонаправлены 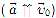и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов 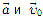противоположны 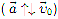и проекция ускорения на направление движения отрицательна.

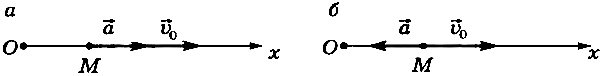
Рис. 6

Вектор 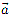при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости 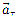и перпендикулярно скорости 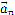(рис. 7), 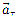— тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, 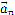— нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения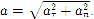

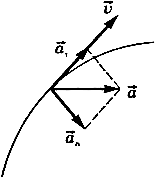
Рис. 7

В робототехнике, есть две основные задачи кинематики:
прямая и обратная.

Рассмотрим эти задачи на стандартном примере манипулятора.

Прямая задача — это вычисление положения (X, Y, Z) рабочего органа манипулятора по его кинематической схеме и заданной ориентации (A1, A2… An) его звеньев (n — число степеней свободы манипулятора, A — углы поворота).

Обратная задача — это вычисление углов (A1, A2… An) по заданному положению (X, Y, Z) рабочего органа и опять же известной схеме его кинематики.

Т.о., решение прямой задачи говорит — где будет находиться рабочий орган манипулятора, при заданных углах его суставов, а обратная задача, наоборот, говорит: как нужно «вывернуться» манипулятору, чтобы его рабочий орган оказался в заданном положении.

Очевидно, что более распространённой и важной является именно обратная задача кинематики.
Но нужно иметь в виду, что эта задача редко может быть решена однозначно.
Дело в том, что хотя для углов (A1, A2,..., An) всегда существует ЕДИНСТВЕННОЕ положение (X, Y, Z) рабочего органа, но не факт, что для положения (X, Y, Z) отыщется такая же единственная комбинация углов (A1, A2,..., An).
Скорее всего, достичь заданного положения (X, Y, Z) возможно и при другой комбинации углов (A1', A2',..., An').
При решении обратной задачи аналитически, эта неоднозначность проявляется в явном виде (например, через квадратные корни).