Теорема о кинетической энергии.

Распишем выражение для работы (5.1), воспользовавшись вторым законом Ньютона:

. (5.4)

Физическая величина, равная:

, (5.5)

называется кинетической энергией. Отметим, что в разных инерциальных системах отсчета скорость тела может быть разной. Следовательно, кинетическая энергия зависит от выбора инерциальной системы отсчёта. Здесь же отметим, что кинетическая энергия – величина аддитивная. Из формулы (5.4) следует, что элементарная работа равнодействующей всех сил равна полному дифференциалу от кинетической энергии. Если в результате действия силы скорость тела изменилась от v ₁ до v ₂, то, интегрируя выражение (5.4), получаем:

. (5.6)

Или, приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, под действием которых совершалось это перемещение.

Формулу (5.6) называют теоремой о кинетической энергии. [6] Из формулы (5.6) следует, что кинетическая энергия измеряется, как и механическая работа, в джоулях.

Теперь рассмотрим тело массы m, которое вращается с угловой скоростью ω вокруг неподвижной оси. Кинетическую энергию найдём, просуммировав кинетические энергии малых частичек массы m_i, на которые разобьем тело:

.

Здесь r _і – расстояние от i -й частицы до оси вращения. Таким образом, кинетическая энергия вращающегося тела

. (5.7)

И опять отметим подобие формул для поступательного и вращательного движений – на это раз кинетических энергий поступательного (5.5) и вращательного движений (5.7).

Теперь можно легко найти выражение для работы равнодействующей всех сил при вращении тела вокруг неподвижной оси. На основании теоремы о кинетической энергии (5.6) имеем:

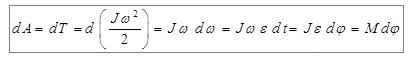. (5.8)

Здесь мы воспользовались основным законом динамики вращательного движения (4.9) M = J ε, а также учли, что 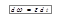. Из формулы (5.8) следует, что при вращательном движении работа совершается моментом сил.

В случае плоского сложного движения кинетическая энергия тела будет состоять из двух частей – кинетической энергии поступательного движения его центра масс и кинетической энергии вращения вокруг центра масс с угловой скоростью ω:

. (5.9)