
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
При постоянной температуре
|
|
Адсорбцию газа можно характеризовать:
1. Зависимостью количества адсорбированного вещества а от температуры при постоянном равновесном давлении р. Кривые а = f(p) называются изобарами адсорбции. Выше отмечалось, что при физической адсорбции с повышением температуры адсорбция уменьшается: da / dT < 0.
2. Зависимостью количества адсорбированного вещества от равновесного давления при постоянной температуре. Графики а = f(p) при Т = const называются изотермами адсорбции. Изотермы имеют решающее значение при изучении адсорбции, поэтому мы будем рассматривать именно эти кривые.
На рис. 4.1. представлены типичные изотермы физической адсорбции при двух температурах.
Изотермы имеют три участка. Начальный почти прямолинейный участок I свидетельствует о том, что при малых давлениях адсорбция практически пропорциональна давлению. Это отвечает ситуации, когда поверхность адсорбента практически свободна. Горизонтальный участок III показывает, что при больших давлениях адсорбция практически не зависит от давления. Это связано с тем, что поверхность уже насыщена адсорбтивом. Промежуточный участок кривой II соответствует частичному заполнению поверхности.

Рис. 4.1. Изотермы адсорбции при двух температурах
1 – изотерма при температуре T1;
2 – изотерма при температуре T2
T1< T2
В соответствии со сказанным выше о влиянии температуры на адсорбцию верхняя кривая на рис. 4.1, отвечающая более низкой температуре, лежит выше нижней.
Для аналитического описания адсорбции Фрейндлих вывел эмпирическое уравнение:
 (4.1)
(4.1)
где b и 1/n – константы, зависящие от природы газа и температуры и не зависящие от равновесного давления газа в системе.
Уравнение Фрейндлиха представляет собой уравнение параболы. С его помощью можно описать не всю изотерму, а только ее криволинейный участок II. Для линейного участка I константа 1/n должна быть равной единице. Тогда уравнение Фрейндлиха примет вид:
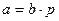 (4.2)
(4.2)
Таким образом, величина адсорбции при малых давлениях газа прямо пропорциональна давлению (закон Генри)/
Для описания горизонтального участка III константа 1/n должна быть равна нулю. Тогда  .
.
Итак, уравнение Фрейндлиха справедливо только для криволинейного участка изотермы.
Постоянные в уравнений Фрейндлиха b и 1/n находят на основе опытных данных. Для этого степенное уравнение логарифмируют.

В координатах ln a—ln p— это уравнение прямой (рис. 4.2), не проходящей через начало координат. Тангенс угла наклона  равен 1/n, а отрезок, отсекаемый ею на оси ординат, равен ln b. Уравнение Фрейндлиха часто используется при обработке экспериментальных результатов. Следует отметить, что для описания адсорбции на твердых адсорбентах справедливо также фундаментальное уравнение Гиббса (3.1), однако практическое применение этого уравнения затруднено из-за невозможности непосредственного измерения поверхностного натяжения на границе «твердое тело-газ».
равен 1/n, а отрезок, отсекаемый ею на оси ординат, равен ln b. Уравнение Фрейндлиха часто используется при обработке экспериментальных результатов. Следует отметить, что для описания адсорбции на твердых адсорбентах справедливо также фундаментальное уравнение Гиббса (3.1), однако практическое применение этого уравнения затруднено из-за невозможности непосредственного измерения поверхностного натяжения на границе «твердое тело-газ».

Рис. 4.2. Изотерма адсорбции в логарифмических координатах