
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Адсорбции Ленгмюра. Эту теорию мы рассматривали применительно к адсорбции раетворенного вещества на поверхности жидкости (см
|
|
Эту теорию мы рассматривали применительно к адсорбции раетворенного вещества на поверхности жидкости (см. параграф 3.6). При разработке теорий мономолекулярной адсорбции газа на твердом адсорбенте И. Ленгмюр исходил из следующих допущений:
1. адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центpax, каждый из которых взаимодействует лишь с одной молекулой газа; в результате образуется мономолекулярный слой;
2. адсорбционные центры энергетически эквивалентны – поверхность адсорбента эквипотенциальна;
3. адсорбированные молекулы не взаимодействуют между собой;
4. адсорбцию газа на твердом адсорбенте можно рассматривать как квазихимическую реакцию, уравнение которой можно записать так:
молекула газа + активный центр  адсорбционный комплекс.
адсорбционный комплекс.
С увеличением концентрации (давления) газа равновесие сдвигается в сторону образования адсорбционного комплекса и свободных активных центров становится меньше.
Константа адсорбционного равновесия:
 (4.4)
(4.4)
где  – концентрация образовавшегося на поверхности комплекса;
– концентрация образовавшегося на поверхности комплекса;  – концентрация активных центров; сB – концентрация газа.
– концентрация активных центров; сB – концентрация газа.
Но концентрация комплекса на поверхности – это величина адсорбции, т.е.:
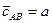 (4.5)
(4.5)
 (4.6)
(4.6)
где 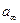 – емкость адсорбционного монослоя, т. е. число адсорбционных центров, приходящихся на единицу площади поверхности или на единицу массы адсорбента. Подставляя (4.5) и (4.6) в уравнение (4.4), получим:
– емкость адсорбционного монослоя, т. е. число адсорбционных центров, приходящихся на единицу площади поверхности или на единицу массы адсорбента. Подставляя (4.5) и (4.6) в уравнение (4.4), получим:
 или
или  (4.7)
(4.7)
Решаем уравнение (4.7) относительно а:
 (4.8)
(4.8)
Выражение (4.8) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, изотерма Ленгмюра принимает вид:
 (4.9)
(4.9)
Уравнение Ленгмюра хорошо описывает изотерму адсорбции (рис.4.1), давая при малых и больших давлениях на графике приблизительно прямолинейные участки, чего не дает уравнение Фрейндлиха. Действительно при малых давлениях в знаменателе уравнения (4.9) можно пренебречь величиной Кр по сравнению с единицей. Тогда
 (4.10)
(4.10)
Уравнение Ленгмюра принимает вид, тождественный уравнению (4.2), и соответствует начальному участку изотермы. При больших давлениях р в знаменателе (4.9) можно пренебречь единицей по сравнению с К*р, тогда  , т.е. адсорбированное количество вещества не зависит от давления, что отвечает прямолинейному участку изотермы, параллельному оси абсцисс.
, т.е. адсорбированное количество вещества не зависит от давления, что отвечает прямолинейному участку изотермы, параллельному оси абсцисс.
Уравнение Ленгмюра может быть решено графически. Перенесем числитель в уравнении (4.9) в знаменатель, а знаменатель – в числитель:
 (4.11)
(4.11)
Умножим обе части уравнения (4.11) на р:
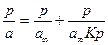 (4.12)
(4.12)
В координатах  – р это уравнение прямой (рис. 4.3). Котангенс угла наклона прямой к оси абсцисс равен
– р это уравнение прямой (рис. 4.3). Котангенс угла наклона прямой к оси абсцисс равен 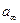 , а отрезок, отсекаемый прямой на оси ординат, равен
, а отрезок, отсекаемый прямой на оси ординат, равен  .
.

Рис. 4.3. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра
Таким образом, построив по экспериментальным данным график, представленный на рис. 4.3, можно определить предельную адсорбцию 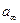 , а затем – константу адсорбционного равновесия К.
, а затем – константу адсорбционного равновесия К.
С помощью теории мономолекулярной адсорбции можно описать ступенчатую адсорбцию, изотерма которой представлена на рис. 4.4. Характер изотермы легко объяснить, если принять, что на поверхности адсорбента имеются группы активных центров, резко отличающихся по своей адсорбционной активности. Так, I ступень отвечает заполнению более активных центров, II ступень – заполнению следующих по активности центров и т. д.
Рис. 4.4. Изотерма ступенчатой адсорбции
Уравнение Ленгмюра можно использовать только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. Это условие выполняется достаточно строго при хемосорбции и физической адсорбции газов при небольших давлениях и температурах выше критической (в отсутствии конденсации на поверхности адсорбента).
Опыт показывает, что наряду с изотермами адсорбции, представленными на рис. 4.1 и 4.4, встречаются S-образные изотермы, на которых нет участка, параллельного оси давлений и отвечающего насыщению поверхности адсорбента молекулами адсорбтива. Вид таких изотерм представлен на рис. 4.5. В связи с необходимостью объяснения характера таких изотерм возникла потребность в других теориях
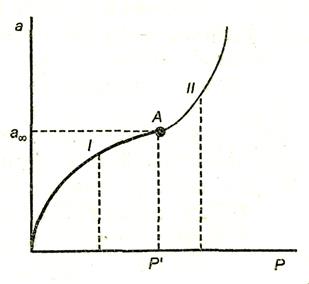
Рис. 4.5. Вобразная изотерма адсорбции