Показатели вариации признака. Свойства и методы расчета показателей вариации

Средняя величина дает обобщающую характеристику все совокупности изучаемого явления. Однако два распределения, имеющие одинаковую среднюю арифметическую, могут значительно отличаться друг от друга по степени рассеяния (вариации) признака. Если индивидуальные значения признака ряда мало отличаются друг от друга (рис.7.1, а), то средняя арифметическая будет достаточно надежной показательной характеристикой типичного уровня в данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака (рис. 7.1, б), то средняя арифметическая будет ненадежной характеристикой типичного уровня этой совокупности и ее практическое применение будет ограничено.

Рисунок 7.1 - Примеры различных типов вариации признака X

Для измерения рассеяния (вариации) признака применяются различные абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся следующие.

• Размах вариации R, который представляет собой разность между максимальным и минимальным значениями признака в совокупности: R = .Недостатком данной показателя является то, что размах вариации показывает лишь крайние отклонения признака и не отражает отклонений все вариантов значений признака.

Среднее по совокупности отклонение значения признака от его среднего уровня измеряют два следующих показателя вариации: среднее линейное и среднее квадратическое отклонение.

• Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда полагают, что среднюю вычитают из варианта):

- невзвешенное среднее линейное отклонение;

- взвешенное среднее линейное отклонение,

где n — объем совокупности; f — частота в i -й группе (у i -ro варианта значения признака).

Математические свойства модулей плохие, поэтому часто на практике применяют другой показатель среднего отклонения от средней — среднее квадратическое отклонение.

• Среднее квадратическое отклонение σ представляет собой среднюю квадратическую из отклонений отдельных вариантов от их средней арифметической:

- невзвешенное;

- взвешенное.

Среднее линейное и отклонение показывают, как расположена основная масса единиц совокупности относительно среднего арифметического значения; они выражаются в тех же единицах, что и варианты (X ), поэтому экономически хорошо интерпретируются.

• Дисперсия σ ² — это квадрат среднего квадратического отклонения. Она представляет собой средний квадрат отклонений вариантов от их средней величины. Она может быть также вычислена, как разность среднего квадрата значения признака и квадрата среднего арифметического значения признака.

Дисперсия вычисляется по простой невзвешенной и взвешенной:

- невзвешенная;

- взвешенная.

Среднее квадратическое отклонение и дисперсия входят в большинство теорем теории вероятности и математической статистики, что обусловливает их широкое применение на практике. Кроме того, дисперсия может быть разложена на составные части, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

Основные вычислительные свойства дисперсии:

1) дисперсия постоянной величины равна 0;

2) если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменится;

3) если все варианты значений признака уменьшить в одно и то же число А раз (А — const), то дисперсия уменьшится в А² раз.

При вычислении показателей вариации сгруппированных данных используют формулу взвешенной средней. Для интервальных рядов распределения в качестве вариантов значений признака используют центральные (серединные) значения. В результате получают приближенные значения статистических показателей.

Относительные показатели вариации применяют, если необходимо оценить интенсивность вариации, или сравнить вариацию признака в различных совокупностях, или сравнить вариацию различных признаков. Показатель относительной вариации рассчитывается как отношение абсолютного показателя вариации к среднему значению.

К относительным показателям вариации относятся:

1) коэффициент осцилляции ;

2) линейный коэффициент вариации ;

3) простой коэффициент вариации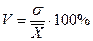

Эти показатели выражаются в процентах или относительных величинах.

Самым распространенным относительным показателем рассеяния является коэффициент вариации V. Он представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

.

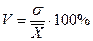Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает33%.