Взаимосвязи общественных явлений, их виды и формы

Признаки, которыми характеризуются единицы совокупности, могут быть взаимосвязанными. Взаимосвязанные признаки выступают в одной из ролей:

§ роли признака-результата (аналог зависимой переменной Y в математике);

§ роли признака-фактора, значения которого определяют значение признака-результата (аналог независимой переменной X в математике).

Связи классифицируют по степени тесноты, направлению, форме, числу факторов.

По степени тесноты связи делят на статистические и функциональные.

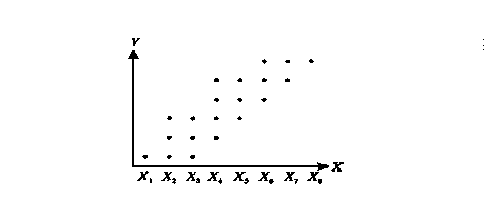
Статистическая (стохастическая) связь — это такая связь между признаками, при которой для каждого значения признака-фактора X признак-результат Y может в определенных пределах принимать любые значения с некоторыми вероятностями; при этом его статистические (массовые) характеристики (например, среднее значение) изменяются по определенному закону (рисунок 9.1).

Статистическая связь обусловлена:

1) влиянием на результативный признак не только фактора X, но и других факторов;

Рисунок 9.1 - Статистическая связь между признаками X и Y

2) неизбежностью ошибок измерения значений признаков (X и Y).

Модель стохастической связи может быть представлена в общем виде уравнением:

Y=f(X, и),

где Y — фактическое значение результативного признака;

f(X) — часть результативного признака, сформировавшаяся под воздействием фактора X (или множества факторов: Y = f (,..., );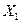

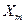и — случайная составляющая, часть результативного признака, возникшая вследствие действия прочих (неучтенных) факторов, а также ошибок измерения признаков.

Например, уровень успеваемости студентов по статистике стохастически связана с целым комплексом факторов: склонностью к точным наукам; временем, затраченным на подготовку к предмету, состоянием здоровья студента и др. Полный перечень факторов неизвестен. Кроме того, неодинаково действие любого известного фактора на успеваемость каждого студента. Например, при одной и той же успеваемости разные студенты затрачивают неодинаковое время на подготовку. Кроме того, при одинаковых возможностях наблюдается вариация значений успеваемости студентов.

Корреляционная связь — частный случай статистической связи. При корреляционной связи с изменением значения признака переднее значение признака Y закономерно изменяется, в то время как в каждом отдельном случае признак Y (с различными вероятностями) может принимать множество различных значений. Модель корреляционной связи: Е(Y\X) == f (Х) или Е (Y| , ,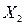..., 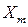) =f(, ,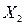..., 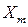), т – количество факторов, Е — математическое ожидание.

Противоположностью статистической связи является функциональная.

Функциональная связь — такая связь, когда каждому возможному значению признака-фактора X соответствует одно или несколько строго определенных значений результативного признака Y (рисунок 9.2). Она имеет место, когда все факторы, действующие на результативный признак, известны и учтены в модели и ошибки измерения отсутствуют.

Модель функциональной связи может быть представлена как:

.

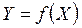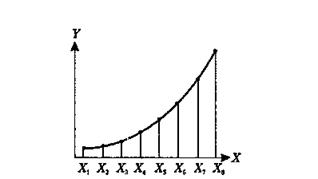
Рисунок 9.2 - Функциональная связь между признаками X и Y

Чаще всего функциональные связи наблюдаются в явлениях, описываемых математикой, физикой и другими точными науками. Функциональные связи имеют место и в социально-экономических процессах, но довольно редко. Примером функциональной связи в экономике может служить связь между показателем фондовооруженности персонала — Y и показателями стоимости основных производственных фондов — X₁ и численностью промышленно-производственного персонала — Х₂. Для любого предприятия наблюдается следующая зависимость между показателями: Y = X_t/X₂.

По направлению связи делятся на прямые и обратные.

При прямой связи направление изменения результативного признака совпадает с направлением изменения признака-фактора.

При обратной связи направление изменения результативного признака противоположно направлению изменения признака-фактора.

Например, чем выше квалификация рабочего, тем выше уровень производительности его труда (прямая связь). Чем выше производительность труда, тем ниже себестоимость единицы продукции (обратная связь).

По форме связи (виду функции f) связи делят на линейные (прямолинейные) и нелинейные (криволинейные) связи.

Линейная связь отображается прямой линией; криволинейная — кривой (параболой, гиперболой и т. п.). При линейной связи с возрастанием значения факторного признака происходит равномерное возрастание (убывание) значения результативного признака. При криволинейной связи свозрастанием значения факторного признака возрастание (убывание) результативного признака происходит неравномерно (гиперболическая форма связи) или же направление его изменения меняется на обратное (параболическая форма связи).

По количеству факторов, действующих на результативный признак, связи подразделяют на однофакторные (парные) и многофакторные связи.

Порядок изучения статистической связи.

1.Качественный (содержательный) анализ связи. На этом этапе определяется состав признаков, связь между которыми будет анализироваться. Здесь же производят предварительный анализ формы связи.

2.Сбор данных (статистическое наблюдение).

3.Количественная оценка тесноты связи по эмпирическим данным.

Если оценивается взаимосвязь качественных признаков, то данный этап является заключительным.

Если оценивается взаимосвязь количественных признаков, то подтверждение гипотезы о наличии взаимосвязи является основанием для перехода к этапу 4.

4. Установление аналитической зависимости между признаками (регрессионный анализ):

1) выбор формы связи (вида аналитического уравнения связи);

2) оценка параметров уравнения;

3) оценка адекватности аналитического уравнения связи эмпирическим данным (оценка качества уравнения).

4) оценка надежности уравнения (с использованием методов теории вероятности и математической статистики).