Уравнение регрессии, определение его параметров

Уравнение регрессии — это уравнение, описывающее корреляционную зависимость между признаком-результатом Y и признаками факторами (одним или несколькими).

Наиболее часто для описания статистической связи признаков используется линейное уравнение регрессии. Внимание к линейной форме связи объясняется четкой экономической интерпретацией параметров линейного уравнения регрессии, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Линейное парное уравнение регрессии имеет вид

, где n —объем совокупности (число наблюдений).

Оценки параметров линейной регрессии (а и b) могут быть найдены разными методами. Наиболее распространенным является метод наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака — Y от расчетных (теоретических) значений — (рассчитанных по уравнению регрессии) минимальна:

.

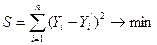В случае линейной парной зависимости:

Значения Y и Y i =1, п нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров — а и b. Чтобы найти минимум функции двух переменных, необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их к нулю, т.е.

.

В результате получим систему из двух нормальных линейных уравнений:

.

Решая данную систему, найдем искомые оценки параметров:

.

Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм 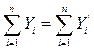(возможно некоторое расхождение из-за округления расчетов).

Параметр b может быть рассчитан также через коэффициент корреляции:

.

Знак коэффициента регрессии b указывает направление связи (если b > О, то связь прямая, если b < О, то связь обратная). Величина b показывает, на сколько единиц изменится в среднем признак-результат Y при изменении признака-фактора X на 1 единицу своего измерения.

Формально значение параметра а — среднее значение признака-результата Y при значении признака-фактора Х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла.