Внутригрупповая и межгрупповая вариация.

Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой, т.е. расчленяют по нему всю совокупность на группы и определяют, как изменяется, варьирует общий результат под влиянием фактора, положенного в основание группировки.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

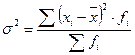
Вариация, обусловленная фактором, положенным в основание группировки, называется межгрупповой вариацией. Размеры ее определяются при помощи дисперсии групповых средних. Межгрупповая дисперсия δ ² характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающее под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:

,

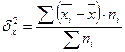где и 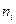- соответственно средние и численности по отдельным группам.

Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем среднюю из внутригрупповых дисперсий:

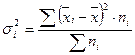- внутригрупповая дисперсия;

- средняя из внутригрупповых дисперсий.

Средняя из внутригрупповых дисперсий характеризует случайную вариацию, которая возникает под влиянием всех факторов, кроме положенного в основание группировки. Чтобы определить ее, надо рассчитать вначале внутригрупповые дисперсии по каждой группе в отдельности, а затем среднюю из них.

Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

.

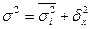Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида