Задачи изучения множественной связи

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на результат, можно пренебречь. В экономике (в отличие от естественных наук) невозможно контролировать поведение большинства экономических факторов. Влияние данных факторов нужно учитывать в модели. То есть нужно построить уравнение, описывающее множественную связь:

Y=f(X₁, X₂,..., X_m, u),

где Y— признак-результат;

X_1, Х₂,..., Х_т — признаки-факторы; и — случайная составляющая.

Задачи анализа многофакторной зависимости:

1)сравнение степени влияния различных факторов на результат;

2)выделение прямого (непосредственного) влияния фактора на результат и косвенного (опосредованного) влияния фактора на результат (через другие факторы);

3)выявление существенности влияния данного фактора (или группы факторов) на результат на фоне других факторов (т. е. нельзя ли исключить из модели данный фактор без существенного ухудшения описания результирующей переменной).

Изобразим графически связи всех признаков для двухфакторной регрессии: Y=f(X_1, Х₂, и) (рисунок 9.3).

- рямые связи

- полные связи

- косвенные (опосредованные) связи

Неучтенные в модели факторы

Рисунок 9.3 - Граф связей модели: Y=f(X_1, Х₂)

Отбор факторов обычно осуществляется в два этапа.

1.Теоретический (содержательный) анализ взаимосвязи результата и факторов, оказывающих на него существенное влияние.

2.Количественная оценка (расчет соответствующих показателей) и анализ взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции).

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

• Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).

• Каждый фактор должен быть достаточно тесно связан с результатом (при линейной связи коэффициент парной корреляции фактора с результатом должен существенно отличаться от нуля).

• Факторы не должны быть коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — наличие высокой линейной связи между всеми или несколькими факторами.

Мультиколлинеарность может привести к нежелательным последствиям:

1) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы;

2)становится невозможным определить изолированное влияние факторов на результативный показатель;

3)оценки параметров уравнения множественной регрессии могут оказаться ненадежными.

Корреляционная матрица — это квадратная матрица размером (т + 1; т + 1), где т — число факторов в модели. Ее размер определяется числом признаков, участвующих в анализе: т признаков-факторов и один признак-результат.

… … … … … - корреляционная матрица

Анализ корреляционной матрицы позволяет:

• ранжировать факторы по степени их влияния на результат;

• выявить мультиколлинеарные факторы.

Таким образом, анализ корреляционной матрицы позволяет решить вопрос о составе факторов в уравнении множественной регрессии.

Параметры уравнения линейной множественной регрессии:

У'= а + 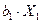+ + …+ (1) можно определить:

1) методом наименьших квадратов, решив систему нормальных линейных уравнений:

(для решения данной системы можно воспользоваться, например, методом Гаусса (определителей));

2) через β -коэффициенты (параметры уравнения регрессии в стандартных масштабах):

, .

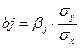Коэффициент регрессии 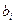при факторе Xj в уравнении (1) называют условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора Xj на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих средних уровнях).

Если не делать предположения о значениях прочих факторов, входящих в модель, то это означает, что каждый из них при изменении Xj может также изменяться (так как факторы (пусть и несильно) связаны между собой). Изменение прочих факторов модели вызовет изменение признака-результата. Таким образом, изменение признака-результата будет обусловлено изменением всех факторов модели, а не только интересующего нас фактора Xj.

Коэффициенты множественной детерминации и корреляции характеризуют совместное влияние всех факторов на результат. Кроме того, они используются как показатели качества уравнения множественной регрессии.

Коэффициент множественной детерминации — это теоретический коэффициент детерминации — для случая множественной регрессии. По аналогии с парной линейной регрессией он определяется как отношение дисперсии признака-результата, объясненной уравнением множественной регрессии — δ *², к общей дисперсии признака-результата — . Область допустимых значений — от нуля до единицы. Данный показатель характеризует долю вариации признака-результата, объясненную уравнением регрессии (а следовательно, и факторами, включенными в данное уравнение), в общей вариации признака-результата.

Для линейного уравнения регрессии данный показатель может быть рассчитан через β -коэффициенты как:

.

Коэффициент множественной корреляции — R рассчитывается как корень из коэффициента множественной детерминации:

.

Данный показатель аналогичен линейному парному коэффициенту корреляции — , используемому в парном регрессионном анализе. Но, в отличие от него, может принимать значения только от нуля до единицы, следовательно, не может служить характеристикой направления связи. Чем плотнее фактические значения 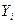располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина . Таким образом, при значении , близком к единице, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении , близком к 0, уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.