Тікелей және жанама өлшеулер кезіндегі қателіктер. Орташа абсолюттік және орташа салыстырмалы қателіктер.

Тікелей ө лшеу – бірдей тә жірибелердің кө мегімен ө лшенетін шамалардың мә ндерін анық тау.

Кездейсоқ қ ателіктердің деректерін ө ң деу жә не параметрлерін бағ алау математикалық статистика ә дістерімен жү ргізіледі.

Орташа арифметикалық мә н немесе ө лшенетін шаманың табылғ ан мә ндерінің орташасы ` х

С тандарттық ауытқ у тү сінігін енгізейік.

х₁, х₂,........х_n ө лшеу нә тижелерінің стандарттық ауытқ уы – бұ л х₁, х₂,........х_n ө лшеу нә тижелерінің орташа қ ателіктерін бағ алау.

Егер орташа` х бұ л х шамасының ең дұ рыс бағ асы болса, онда айырмашылығ ы, -дің - дан ауытқ уы деп аталады, ол -дің ә р мә нінің мә нінен қ аншалық ты ө згешеленетінін кө рсетеді. Егер 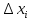ауытқ уы ө те аз болса, онда ө лшеу нә тижелері бір біріне жақ ын болады жә не ө те дә л болуы мү мкін.

х₁, х₂,..., х_n ө лшемдерінің нә тижелерінің сенімділігін бағ алау ү шін барлық ауытқ улардың квадратын шығ арамыз, содан кейін осы сандардың орташасын аламыз. Егер енді алынғ ан нә тижелерден квадрат тү бірді шығ аратын болсақ, онда х шамасының ө зінің бірлігінде ө лшенетін шаманы аламыз. Бұ л сан х₁, х₂,........х_n стандартты ауытқ уы деп аталады жә не деп белгіленеді:

Сонымен, стандартты ауытқ у (СА) х₁, х₂,.., х_n ө лшеу нә тижелерінің орташа квадраттық ауытқ уы болып табылады.

-ның квадратын ала отырып, біз дисперсия деп аталатын шаманы аламыз.

Алынғ ан пікірлерден кө ретініміз, х шамасының ө лшемдерінің саны кө п болғ ан кезде шамамен нә тижелердің 70 пайызы интервалында жататын болады. Бір реттік ө лшем (сол аппаратурамен алынғ ан) нақ ты мә ннен -тан астамғ а ө згешеленбейтінін 70 пайызғ а тең ық тималдылық пен кө рсетуге болады.

Физикалық шамалардың кө пшілігін ә детте тікелей ө лшеу мү мкін емес жә не оларды анық тауғ а екі ә р тү рлі кезең кіреді.

Алдымен тікелей ө лшенуі мү мкін біреуін немесе х, у,... бірнешеуін ө лшейді.

Содан кейін тікелей ө лшенген шамалардың мә ндерін пайдалана отырып, ізделіп отырғ ан шаманың ө зін есептейді. Мысалы, тік бұ рыштың ауданын табу ү шін, ә детте оның ұ зындығ ын (l) жә не биіктігін (һ) ө лшейді жә не содан кейін мына формула бойынша оның ауданын есептейді.

Егер ө лшемге осы екі кезең кірсе, онда қ ателіктерді бағ алауғ а да олар кіреді.

Алдымен тікелей ө лшенетін шамалардағ ы қ ателіктерді бағ алау керек, содан кейін осы қ ателіктер есептеулерге қ алай «таралатындығ ын» жә не соң ғ ы нә тижелерде қ ателіктерге ә келетінін айқ ындау керек. (Нә тижелік қ ателіктерді есептеу ү шін басқ а ә діс. Егер барлық ө лшеулерді бірнеше рет қ айталауғ а болатын болса жә не егер табиғ аты бойынша барлық қ ателіктер кездейсоқ болатынына сенімділік болса, онда мү дделі шамадағ ы жанама ө лшеулердегі қ ателікті орташа арифметикалық тан орташа квадраттық ауытқ у арқ ылы бағ алауғ а болады).

Сонымен, жанама ө лшеулер – бұ л q іздеп отырғ ан шаманың мә нін белгілі тә уелділік негізінде табатын ө лшем 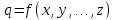, мұ нда - тікелей ө лшем кезінде алынғ ан мә ндер.

Функциональдық тә уелділіктің f тү рі бойынша олар екі негізгі – сызық тық жә не сызық тық емес топқ а бө лінеді.

шамалары қ ателіктерімен ө лшенген жә не ө лшенген мә ндер функциясын есептеу ү шін пайдаланылады деп болжайық. Егер қ ателіктері тә уелсіз жә не кездейсоқ болса, онда q-нің қ ателігі мынағ ан тең:

мұ нда,

- жанама ө лшеудің абсолютті қ ателігі;

, - аргументтерді ө лшеу нә тижелерінің орта мә ннен ауытқ уы;

дегеніміз бойынша q функциясының дербес туындылары.

Ө лшеу процедурасы келесі кезең дерден тұ рады: ө лшеу объектісінің ү лгісін таң дау, ө лшеу тә сілін таң дау, Ө Ж таң дау, нә тиже алу ү шін тә жірибе жү ргізу. Бұ л ө лшеу нә тижесі ө лшенетін шаманың нақ ты мә ні ө лшеу қ ателігі деп аталатын қ андай да бір шамағ а ө згеретініне ә кеп соғ ады. Ө лшенетін шама анық талып, оның нақ ты мә ннен ауытқ уы мү мкін дә режесі анық талғ ан болса ө лшеу аяқ талды деп есептеуге болады.

Қ ателіктің пайда болу себептері ө те коп, сондық тан олардың жіктелуі шартты сипатқ а ие.

Ө Ж қ ателігі мен осы Ө Ж-мен ө лшеу нә тижесінің қ ателігін ажырата білу керек. Ө лшеу қ ателігі қ олданылатын Ө Ж-нің метрологиялық сипатына, алынғ ан ө лшеу тә сіліне, сыртқ ы жағ дайларғ а, сондай-ақ ө лшенетін шама мен объект қ асиеттеріне тә уелді. Ө лшеу қ ателігі қ олданылатын Ө Ж қ ателігінен ә детте жоғ ары болады, бірақ қ ателіктерді болдырмау тә сілдерімен жә не кө преттік бақ ылау деректерін статистикалық ө ң деу арқ ылы кейбір жағ дайларда ө лшеу қ ателігін қ олданылатын Ө Ж қ ателігінен азайтып алуғ а болады.

Ө рнектелу тә сілі бойынша қ ателіктер абсолюттік, салыстырмалы жә не келтірілген болып жіктеледі.

Абсолюттік қ ателік — ө лшенетін физикалық шама бірлігімен ө рнектелетін Ө Ж қ ателігі:

Δ = Х _изм – Х_д . (1.3)

Салыстырмалы қ ателік — ө лшеу қ ұ ралының абсолюттік қ ателігінің ө лшеу нә тижесіне немесе ө лшенген физикалық шаманың нақ ты мә ніне қ атынасымен ө рнектелетін Ө Ж қ ателігі:

γ _отн = (Δ /Х_д)100. (1.4)

Ө лшеу қ ұ ралы ү шін γ _отн шкаланың берілген нү ктесіндегі қ ателікті сипаттайды, ол ө лшенетін шама мә ніне тә уелді жә не қ ұ рал шкаласының ең кіші мә ніне ие.

Кө птеген ө лшеу қ ұ ралдарының сипаттамасы ү шін келтірілген қ ателік қ олданылады.

Келтірілген қ ателік - Ө Ж абсолюттік қ ателігінің барлық ө лшеу диапазонында тұ рақ ты шамасының шартты алынғ ан мә ніне қ атынасымен ө рнектелетін салыстырмалы қ ателік:

γ _прив = (Δ /Х_норм)100, (1.5)

мұ ндағ ы Х_норм— мө лшерлейтiн мә н, яғ ни қ ателік есептелетін қ атынас бойынша анық талатын орнатылғ ан мә н.