Формула касательной к плоскости и нормали

Определение 1. Касательной плоскостью к поверхности в данной точке P (x ₀, y ₀, z ₀) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.

Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка P (x ₀, y ₀, z ₀) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р.

Пусть х = х (t), у = у (t), z = z (t) – параметрические уравнения линии L.

Предположим, что: 1) функция F (х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю; 2) функции х (t), у (t), z (t) также дифференцируемы.

Поскольку кривая принадлежит поверхности s, то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [ x (t), у (t), z (t)] = 0.

Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и в точке P (x ₀, y ₀, z ₀):

.

Пусть точке Р соответствует значение параметра t ₀, то есть x ₀ = x (t ₀), y ₀ = y (t ₀), z ₀ = z (t ₀). Тогда последнее соотношение, вычисленное в точке Р, примет вид

. (17)

Формула (17) представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор

,

не зависящий от выбора кривой на поверхности .

Второй вектор – касательный в точке Р к линии L, а значит, зависящий от выбора линии на поверхности, то есть является переменным вектором.

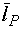При введённых обозначениях равенство (17) перепишем как . Его смысл таков: скалярное произведение равно нулю, следовательно, векторы и перпендикулярны. Выбирая всевозможные кривые (см. рис. 54), проходящие через точку Р на поверхности s, мы будем иметь различные касательные векторы, построенные в точке Р к этим линиям; вектор же от этого выбора не зависит и будет перпендикулярен любому из них, то есть все касательные векторы

расположены в одной плоскости, которая, по определению, является касательной к поверхности s, а точка Р в этом случае называется точкой касания. Вектор является направляющим вектором нормали к поверхности.

Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:

; (18)

(18) – уравнение касательной плоскости, построенной в точке P (x ₀, y ₀, z ₀) к поверхности s, заданной уравнением F (х, у, z) = 0;

; (19)

19. – уравнение нормали, построенной в точке Р к поверхности s.