
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выводить формулы, использующие понятие определенного интеграла для его геометрических и механических приложений.
|
|
Геометрический смысл определенного интеграла. Если f (x) непрерывна и положительна на [ a, b ], то интеграл


представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x) (см. рис. 5.).

Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f (x), заданная на промежутке [ a, b ], равна нулю во всех точках этого промежутка, кроме конечного числа точек z 1, z 2,..., zN. Составим для f (x) интегральную сумму σ.
Пусть из точек ξ 0, ξ 1,..., ξ n -1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f (zi) | (i = 1, 2,..., N) есть K, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ,
откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл


существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть φ (x) задана на промежутке [0, 1] так:



Если мы, составляя сумму σ, за точки ξ k выберем числа иррациональные, то окажется σ = 0. Если же все ξ k взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл
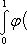

не существует.