Выводить формулы замены переменной и интегрирования по частям для неопределенного интеграла

Метод замены переменной

Теорема. Пусть F (z) есть на каком-нибудь промежутке [ p, q ] первообразная функция для функции f (z). Если φ (x) есть дифференцируемая функция, заданная на промежутке [ a, b ] и удовлетворяющая неравенствам p ≤ φ (x) ≤ q, то сложная функция F [ φ (x)] будет первообразной для функции f [ φ (x)] φ '(x).

В самом деле, дифференцируя сложную функцию y = F [ φ (x)], мы должны ввести промежуточный аргумент z = φ (x). Тогда y = F (z), z = φ (x) и y’_x=y’_z*z’_x=F’(z)ϕ ’(x).Так как F '(z) = f (z), то y’_x=f(z)ϕ ’(x)=f[ϕ (x)]ϕ ’(x), чем и доказана теорема.

Доказанную теорему можно формулировать и так: если

То

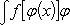
Отсюда следует

Первое правило подстановки. Чтобы вычислить интеграл

записывая его в форме

заменяем здесь φ (x) на z, вычисляем полученный интеграл и в найденном ответе производим обратную замену z на φ (x).