Знать определение первообразной и доказывать теорему, что две первообразные одной и той же функции отличаются на постоянную

Функция F(x) называется первообразной от функции f(x) на отрезке [а, b], если во всех точках этого отрезка выполняется равенство F’(x)=f(x)

Пример: пусть . Тогда 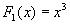первообразная, так как .Функция также первообразная, так как .

Уже из этого примера видно, что у одной функции 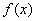может быть несколько первообразных. Чем же эти первообразные отличаются друг от друга?

Теорема. Пусть 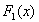и две первообразные одной и той же функции 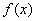.Тогда 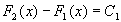, где С- постоянная величина (константа).

Доказательство

Действительно, в этом случае и по теореме о постоянстве функции F2(x)-F1(x)=C

Определение 2. Совокупность всех первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается интеграл f(x)dx.

Функция f(x) называется подинтегральной функцией, а комбинация f(x)dx- подинтегральным выражением.

Пусть F(x) есть какая-то первообразная функции f(x). Так как две первообразных отличаются только на константу, то

 f(x)dx = F(x)+C

Где С – произвольная константа.

13.Доказывать основные свойства неопределённого интеграла

1. ; –производная неопределенного интеграла равна подынтегральной функции, а его дифференциал–подынтегральному выражению.

Доказательство. Из определения первообразной:

2. – неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.

Доказательство. Из определения первообразной следует, что функция является первообразной для функции следовательно, является неопределенным интегралом от .

Например,

3. 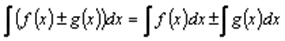–неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от этих функций.

Доказательство. Достаточно показать, что совпадают производные левой и правой частей равенства.

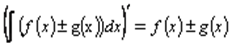–по свойству 1;

.

4. , где k = const –постоянный множитель можно вынести за знак неопределенного интеграла. Доказывается аналогично свойству 3. Из свойств 1 и 2 следует, что дифференцирование и интегрирование являются взаимно обратными действиями.