
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение.
|
|
Определённый интеграл  численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми  и
и  и графиком функции
и графиком функции  .
.

Пусть  определена на
определена на  . Разобьём
. Разобьём  на части с несколькими произвольными точками
на части с несколькими произвольными точками  Тогда говорят, что произведено разбиение
Тогда говорят, что произведено разбиение  отрезка
отрезка  Далее выберем произв. точку
Далее выберем произв. точку  ,
,  ,
,
Определённым интегралом от функции  на отрезке
на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю
называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения
, если он существует независимо от разбиения  и выбора точек
и выбора точек  , т.е.
, т.е.

Если существует указанный предел, то функция  называется интегрируемой на
называется интегрируемой на  по Риману.
по Риману.
Теорема существования определённого интеграла.
Если функция f (x) непрерывна на отрезке [ a, b ], то она интегрируема по этому отрезку.
Примем это утверждение без доказательства, поясним только его смысл. Интегрируемость функции означает существование конечного предела последовательности интегральных сумм, т.е. такого числа  , что для любого
, что для любого  найдётся такое число
найдётся такое число  , что как только разбиение отрезка удовлетворяет неравенству
, что как только разбиение отрезка удовлетворяет неравенству  , то, независимо от выбора точек
, то, независимо от выбора точек 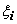 выполняется неравенство
выполняется неравенство 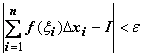 . Требование непрерывности f (x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [ a, b ] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f (x) неограничена на [ a, b ], то она неограничена на каком-либо [ xi -1, xi ], т.е. на этом отрезке можно найти такую точку
. Требование непрерывности f (x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [ a, b ] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f (x) неограничена на [ a, b ], то она неограничена на каком-либо [ xi -1, xi ], т.е. на этом отрезке можно найти такую точку 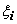 , что слагаемое
, что слагаемое  , а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).
, а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).