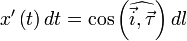Знать определения криволинейных интегралов первого и второго рода и уметь их вычислять

Определения.Пусть — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.

- (отрезок параметризации) — рассматриваем часть кривой.

Пусть — разбиение отрезка параметризации , причем .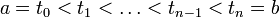

Зададим разбиение кривой .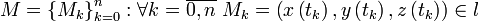

За 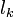обозначим часть кривой от точки до точки , .

Введем мелкость разбиения отрезка параметризации : .

Введем набор промежуточных точек разбиения отрезка параметризации : .

Зададим набор промежуточных точек разбиения кривой .

Пусть нам также даны 4 функции, которые определены вдоль кривой : , , , .

Рассмотрим 4 интегральные суммы.

1) Интегральная сумма криволинейного интеграла первого рода:

.

2) Три интегральных суммы криволинейного интеграла второго рода:

,

,

.

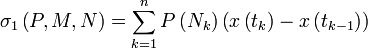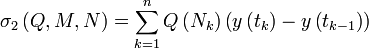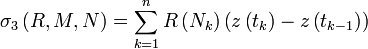Если , то говорят, что функция интегрируема в смысле криволинейного интеграла первого рода по кривой , а сам предел называют криволинейным интегралом первого рода функции по кривой и обозначают 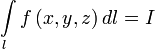. Здесь 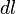— дифференциал кривой.

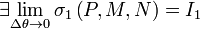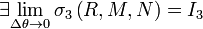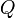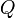Если , , , то говорят, что функции , и интегрируемы в смысле криволинейного интеграла второго рода по кривой , а сами пределы называют криволинейными интегралами второго рода функций , и по кривой и обозначают

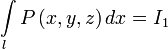
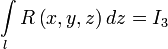
Сумму криволинейных интегралов второго рода функци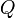й , и также называют криволинейным интегралом второго рода вектор-функции и обозначают:

.

Если кривая замкнута (начало совпадает с концом), то в этом случае вместо значка принято писать .

1 Рода.

Пусть — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла первого рода. Тогда

.

Здесь точкой обозначена производная по : .

2 Рода.

Пусть — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла второго рода. Тогда

,

,

.

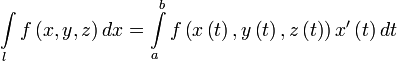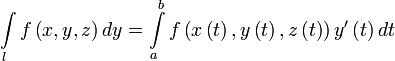Если обозначить за единичный вектор касательной к кривой , то нетрудно показать, что