
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос №14
|
|
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси  , проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами
, проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами  , находящиеся на расстоянии
, находящиеся на расстоянии  от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами
от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами  опишут окружности различных радиусов
опишут окружности различных радиусов  и имеют различные линейные скорости
и имеют различные линейные скорости 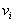 . Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
 (1)
(1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
 .
.
Используя выражение (1), получаем:
 ,
,
где 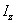 – момент инерции тела относительно оси
– момент инерции тела относительно оси  .
.
Кинетическая энергия при плоском движении.
Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:

| (3.37) |
где  - скорость центра масс тела,
- скорость центра масс тела,  - скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
- скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:

| (3.38) |
так как  (суммарный импульс частиц в системе центра масс равен нулю).
(суммарный импульс частиц в системе центра масс равен нулю).
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.