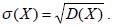Числові характеристики неперервних випадкових величин (НВВ)-математичне сподівання, дисперсія, середнє квадратичне відхилення, початкові та центральні моменти. Властивості НВВ

Геометричний та гіпергеометричний розподіли ДВВ

Геометричний розподіл G(p) з параметром p. Випадкова величина ξ має геометричний розподіл з параметром p p Є (0; 1), якщо вона набуває значення 0, 1, 2, … з ймовірностями 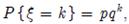або набуває значення 1, 2, 3… з ймовірностями 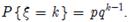При цьому в першому випадку 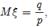у другому - 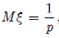, дисперсія - 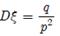в обох випадках.

Гіпергеометричний розподіл. Випадкова величина ξ має гіпергеометричний розподіл з параметром, якщо вона набуває значення 0, 1, 2…min(n, M) з ймовірностями 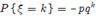або набуває значення 1, 2, 3…з ймовірностями 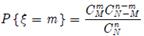, де 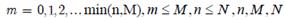- натуральні числа. При цьому .

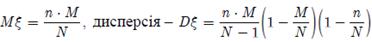Числові характеристики неперервних випадкових величин (НВВ)-математичне сподівання, дисперсія, середнє квадратичне відхилення, початкові та центральні моменти. Властивості НВВ

Як і дискретна, так і неперервна випадкова величина має числові характеристики: математичне сподівання M (X), дисперсію D (X) та середнє квадратичне відхилення σ (X). Математичним сподіванням неперервної випадкової величини, заданої на інтервалі [ a; b] називається визначений інтеграл: 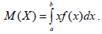Дисперсією неперервної випадкової величини називається математичне сподівання квадрата відхилення її значень від математичного

сподівання: 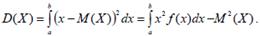Середнім квадратичним відхиленням називається величина, що

знаходиться за формулою: