
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нерівність Чебишева.Теорема Чебишева, її значення для практики.
|
|
Нерівність Чебишова — результат теорії ймовірностей, який стверджує, що для будь-якої випадкової змінної із скінченною дисперсією майже всі значення концентруються біля значення математичного очікування. Нерівність Чебишова дає кількісні характеристики цієї властивості. Нехай  є випадковою змінною із математичним очікуванням
є випадковою змінною із математичним очікуванням 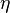 і дисперсією
і дисперсією  . Тоді для всякого
. Тоді для всякого 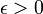 виконується нерівність:
виконується нерівність: 

 З того, що
З того, що  одержуємо твердження теореми.
одержуємо твердження теореми.
Теорема Бернуллістверджує: якщо т - кількість подій А в п попарно незалежних випробуваннях, а р є ймовірність настання події А в кожнім з випробувань, то при будь-якому є> 0 справедлива нерівність Ця формула є першим в історії варіантом закону великих чисел і по суті вважається початком теорії ймовірностей як галузі математичної науки. Теорема Бернуллі дає можливість оцінити кількості незалежних випробувань п при певних умовах їх проведення. У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів. Якщо ймовірність настання події в кожному з випробувань стала, то ймовірність того, що подія настане разів в незалежних випробуваннях дорівнює або 30. Теорема Ляпунова про стійкість. Якщо для системи рівнянь існує знаковизначена функція, похідна якої є знакопостійною функцією протилежного знака, то рішення системи стійке. Теорема Ляпунова про асимптотичну стійкість. Якщо для системи рівнянь існує знаковизначена функція, похідна якої є знаковизначеною функцією, але протилежного знака, то рішення системи буде стійким асимптотично. Теорема Ляпунова про нестійкість. Якщо для системи рівнянь існує яка-небудь функція, похідна якої є знаковизначеною функцією, причому в будь-якому як завгодно малому околі початку координат є область, у якій знак збігається зі знаком рішення системи нестійке. 31.Ланцюги Маркова
Ланцюгом Маркова називається послідовність випробувань, в кожному з яких може відбутися одна і тільки одна із  несумісних подій
несумісних подій  повної групи, причому умовна ймовірність
повної групи, причому умовна ймовірність  того, що в
того, що в  -му випробуванні наступить подія
-му випробуванні наступить подія  за умови, що в
за умови, що в  -му випробуванні появилась подія
-му випробуванні появилась подія  , не залежить від результатів попередніх випробувань. Ланцюг Маркова називається однорідним, якщо умовна ймовірність
, не залежить від результатів попередніх випробувань. Ланцюг Маркова називається однорідним, якщо умовна ймовірність  не залежить від
не залежить від  , в цьому випадку пишуть
, в цьому випадку пишуть  . Якщо для ланцюга Маркова існує стаціонарний (граничний) розподіл, то
. Якщо для ланцюга Маркова існує стаціонарний (граничний) розподіл, то  . В цьому випадку, при
. В цьому випадку, при  ланцюг Маркова входить в стійкий режим, який характеризується властивостями:
ланцюг Маркова входить в стійкий режим, який характеризується властивостями:
а) середній час перебування в стані  дорівнює
дорівнює 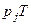 , де
, де  – досить великий проміжок часу;
– досить великий проміжок часу;
б) середній час повернення в стан  дорівнює
дорівнює  ;
;
в) з додатною ймовірністю з будь-якого стану  ланцюг Маркова може перейти у будь-який інший стан
ланцюг Маркова може перейти у будь-який інший стан 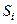 .
.