
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числові характеристики НВВ
|
|
Для НВВ, як і для дискретних, використовуються визначені раніше числові характеристики, але обчислюються вони за іншими формулами. Теорема. Якщо НВВ, що набуває можливих значень з відрізка [a, b], має щільність f(x), то її математичне сподівання знаходять за формулою  Якщо можливі значення Х належать множині дійсних чисел, то
Якщо можливі значення Х належать множині дійсних чисел, то  Теорема. Якщо НВВ набуває можливих значень з відрізку [a, b], то
Теорема. Якщо НВВ набуває можливих значень з відрізку [a, b], то  Якщо можливі значення Х належать множині дійсних чисел, то
Якщо можливі значення Х належать множині дійсних чисел, то  Дисперсію НВВ можна також знайти за формулою
Дисперсію НВВ можна також знайти за формулою  або
або 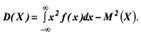 Середнє квадратичне відхилення НВВ визначається та обч за формулою.
Середнє квадратичне відхилення НВВ визначається та обч за формулою.  26 Експоненціальний розподіл — абсолютно неперервний розподіл, що моделює час між двома послідовними завершеннями однієї і тієї ж події.
26 Експоненціальний розподіл — абсолютно неперервний розподіл, що моделює час між двома послідовними завершеннями однієї і тієї ж події.
Випадкова величина  має експоненційний розподіл з параметром
має експоненційний розподіл з параметром  , якщо її густина має вигляд
, якщо її густина має вигляд
 .
.
Щільність експоненціальної випадкової величини  задана першим рівнянням:
задана першим рівнянням:  . Інтегруючи щільність, отримаємо функцію експоненційного розподілу:
. Інтегруючи щільність, отримаємо функцію експоненційного розподілу: 
В теорії ймовірностей і статистиці випадкова величина має дискретний рівномірний розподіл, якщо вона приймає скінченне число значень з однаковими ймовірностями. Якщо випадкова величина може приймати будь-яке з n значень k1, k2, …, kn, тоді це є дискретним рівномірним розподілом. Ймовірність випадання kj дорівнює 1/n. Простим прикладом дискретного рівномірного розподілу є випадання гральної кості. k набуває значень 1, 2, 3, 4, 5, 6 і кожен раз  випадає з імовірністю 1/6. У випадку, коли випадкова величина є дійсним числом, то функція розподілу можна виразити у термінах виродженого розподілу таким чином:
випадає з імовірністю 1/6. У випадку, коли випадкова величина є дійсним числом, то функція розподілу можна виразити у термінах виродженого розподілу таким чином:
 Нормальний розподіл або розподіл Гаусса це розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності.
Нормальний розподіл або розподіл Гаусса це розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності. 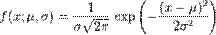 де
де 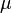 — математичне сподівання,
— математичне сподівання,  — дисперсія випадкової величини. Параметр
— дисперсія випадкової величини. Параметр  також відомий, як стандартний відхил. Розподіл із μ = 0 та σ 2 = 1 називають стандартним нормальним розподілом. Центральна гранична теорема стверджує, що нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Наприклад, відстань від влучення снаряду гармати до цілі при великій кількості пострілів характеризується саме нормальним розподілом. Нормально розподілена випадкова величина позначається так:
також відомий, як стандартний відхил. Розподіл із μ = 0 та σ 2 = 1 називають стандартним нормальним розподілом. Центральна гранична теорема стверджує, що нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Наприклад, відстань від влучення снаряду гармати до цілі при великій кількості пострілів характеризується саме нормальним розподілом. Нормально розподілена випадкова величина позначається так:  .
.