
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Емпірична функція розподілу
|
|
Емпірична функція розподілу. Нехай для вибірки об'єму п з генеральної сукупності ВВ X, функція розподілу якої F(x), побудовано статистичний ряд частот.
Таблиця 1
| хi | х1 | х2 | … | xk |
| пi | n1 | п2 | … | пк |
| Таблиця 2 | ||||
| хi | х1 | х2 | … | xk |
| wi | w1 | w2 | … | wk |
Розподілом вибірки називають дискретну випадкову величину X*, яка приймає значення варіант вибірки xi з ймовірностями pi=ni/n Функцію розподілу величини X* називають емпіричною (вибірковою) функцією розподілу і позначають F*(x). Отже, F*(x) = nx/n, де  - сума частот варіант xi, менших х, п - об'єм вибірки.
- сума частот варіант xi, менших х, п - об'єм вибірки.
Для кожного значення х €(-∞, +∞) F*(x) визначає відносну частоту події X < х, ймовірність цієї події визначає функція F(x) - теоретична функція розподілу. Згідно з законом великих чисел, для будь-якого х €(-∞, +∞) і довільного ε > 0  тобто при кожному х F*(x) збігається по ймовірності до F(x) і, отже, при великому об'ємі вибірки може служити наближеним значенням (оцінкою) функції розподілу генеральної сукупності в кожній точці х.
тобто при кожному х F*(x) збігається по ймовірності до F(x) і, отже, при великому об'ємі вибірки може служити наближеним значенням (оцінкою) функції розподілу генеральної сукупності в кожній точці х.
40. Полігон і гістограмма Якщо досліджувана випадкова величина X дискретна, то для графічного зображення статистичного розподілу вибірки використовують полігон частот (або відносних частот). Полігоном частот називають ламану, відрізки якої сполучають точки (хi; пi) на координатній площині Охп.Полігоном відносних частот називають ламану, відрізки якої сполучають точки (xi, wi) на координатній площині OxW. Для графічного зображення інтервального статистичного ряду будують гістограму частот (відносних частот) - східчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють mi/h. Величину mi/h називають щільністю частоти. Аналогічно будується гістограма відносних частот. Висоти прямокутників у цьому випадку дорівнюють wi/h. Величину wi/h називають щільністю відносної частоти.
41. Статистичні оцінки параметрів розподілу(незміщені, зміщені, ефективні, обгрунтовані)
Статистичні оцінки — це статистики, що використовуються для оцінювання невідомих параметрів розподілів випадкової величини. Наприклад, якщо 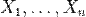 — це незалежні випадкові величини, з заданим нормальним розподілом
— це незалежні випадкові величини, з заданим нормальним розподілом  , то
, то 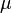 буде середнім арифметичним результатів спостережень.
буде середнім арифметичним результатів спостережень.
Оцінка  параметра
параметра  називається ефективною оцінкою в класі
називається ефективною оцінкою в класі  , якщо для будь-якої іншої оцінки
, якщо для будь-якої іншої оцінки  виконується нерівність
виконується нерівність  для будь-якого
для будь-якого  . Особливу роль в математичній статистиці відіграють незміщені оцінки. Якщо незміщена оцінка
. Особливу роль в математичній статистиці відіграють незміщені оцінки. Якщо незміщена оцінка  є ефективною оцінкою в класі незміщених, то таку статистику прийнято називати просто ефективною.
є ефективною оцінкою в класі незміщених, то таку статистику прийнято називати просто ефективною.
Незміщена оцінка в математичній статистиці — це точкова оцінка, математичне сподівання якої рівне параметру, що оцінюється. Означення - Статистика  називається незміщеною оцінкою параметра
називається незміщеною оцінкою параметра  , якщо
, якщо  .
.
В іншому випадку оцінка називається зміщеною, а випадкова величина  називається її зміщенням.
називається її зміщенням.
Точкова оцінка у математичній статистиці — це число, що обчислюється на основі вибірки, імовірно близьке оцінюваному параметру популяції. Нехай  — випадкова вибірка з розподілу, що залежить від параметра
— випадкова вибірка з розподілу, що залежить від параметра  . Тоді статистику
. Тоді статистику  , що набуває значення в
, що набуває значення в  , називають точковою оцінкою параметра
, називають точковою оцінкою параметра  .
.