
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оцінка математичного сподівання та дисперсії за вибіркою.
|
|
Вибіркові дисперсії s 2, S 2 — це числа. Згідно з теоремою ймовірностей про сталі величини, математичні сподівання цих величин виглядають так:. 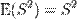 .Вибіркову дисперсію S 2 не можна вважати незміщеною оцінкою генеральної дисперсії σ 2. Дисперсія s 2 є оцінка генеральної дисперсії
.Вибіркову дисперсію S 2 не можна вважати незміщеною оцінкою генеральної дисперсії σ 2. Дисперсія s 2 є оцінка генеральної дисперсії 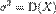 .Дисперсія S 2 — це оцінка генеральної дисперсії
.Дисперсія S 2 — це оцінка генеральної дисперсії  .
.
 44. Методи оцінювання(максимальної правдоподібності, моментів, найменших квадратів) оцінка правдоподібності - Нехай маємо вибірку
44. Методи оцінювання(максимальної правдоподібності, моментів, найменших квадратів) оцінка правдоподібності - Нехай маємо вибірку 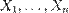 з розподілу
з розподілу 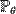 , де
, де 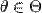 — невідомий параметр. Нехай
— невідомий параметр. Нехай 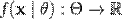 — функція вірогідності, де
— функція вірогідності, де 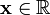 . Точкова оцінка
. Точкова оцінка  називається оцінкою максимальної вірогідності параметра
називається оцінкою максимальної вірогідності параметра  . Таким чином, оцінка максимальної вірогідності — це така оцінка, яка максимізує функцію вірогідності при фіксованій реалізації вибірки. Метод моментів знаходження оцінок в математичній статистиці — це спосіб побудови оцінок, заснований на порівнянні теоретичних і вибіркових моментів. Формально: нехай
. Таким чином, оцінка максимальної вірогідності — це така оцінка, яка максимізує функцію вірогідності при фіксованій реалізації вибірки. Метод моментів знаходження оцінок в математичній статистиці — це спосіб побудови оцінок, заснований на порівнянні теоретичних і вибіркових моментів. Формально: нехай 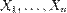 — вибірка з розподілу
— вибірка з розподілу 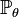 , що залежить від параметра
, що залежить від параметра 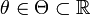 . Нехай маємо функцію
. Нехай маємо функцію  , таку що
, таку що  інтегрована відносно міри
інтегрована відносно міри 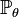 , і
, і  , где
, где 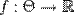 — бієкція. Тоді оцінка
— бієкція. Тоді оцінка 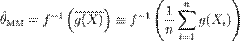 називається оцінкою параметра
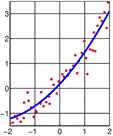
називається оцінкою параметра  методом моментів. Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується в регресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадку системи лінійних рівнянь. Зокрема важливим застосуванням у цьому випадку є оцінка параметрів у лінійній регресії, що широко застосовується у математичній статистиці і економетриці. Нехай маємо лінійну регресію зі скалярною змінною x:
методом моментів. Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується в регресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадку системи лінійних рівнянь. Зокрема важливим застосуванням у цьому випадку є оцінка параметрів у лінійній регресії, що широко застосовується у математичній статистиці і економетриці. Нехай маємо лінійну регресію зі скалярною змінною x: 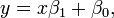 а також вибірку початкових даних
а також вибірку початкових даних  розміру M. Тоді
розміру M. Тоді 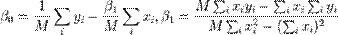 Нехай ми маємо вибірку початкових даних
Нехай ми маємо вибірку початкових даних  . Функція
. Функція 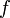 — невідома. Якщо ми знаємо приблизний вигляд функції
— невідома. Якщо ми знаємо приблизний вигляд функції 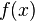 , то задамо її у вигляді функціоналу
, то задамо її у вигляді функціоналу  , де
, де  — невідомі константи. Нам потрібно мінімізувати відмінності між
— невідомі константи. Нам потрібно мінімізувати відмінності між  та
та 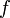 . Для цього беруть за міру суму квадратів різниць значень цих функцій у всіх точках
. Для цього беруть за міру суму квадратів різниць значень цих функцій у всіх точках  і її мінімізують (тому метод так і називається):
і її мінімізують (тому метод так і називається): 
45 Для повного уявлення про точність вимірювань та надійність оцінки випадкових відхилень результатів вимірювань, особливо при обмеженій кількості значень вимірюваної величини, необхідно задатися довірчими межами, довірчим інтервалом та довірчою ймовірністю. Для повного уявлення про точність вимірювань та надійність оцінки випадкових відхилень результатів вимірювань, особливо при обмеженій кількості значень вимірюваної величини, необхідно задатися довірчими межами, довірчим інтервалом та довірчою ймовірністю. Нехай 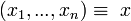 - n незалежних спостережень над випадковою величиною з законом розподілу F(z/a), що залежить від параметра a, значення якого невідомо. Довірчі межі випадкових похибок — це верхня та нижня межі інтервалу, в які похибки потрапляють із заданою ймовірністю Р. Величина Р називається довірчою ймовірністю. Для визначення довірчих меж похибок необхідно знати густину розподілу похибок та ймовірність потрапляння похибок у довірчі межі. Якщо не ввести обмеження, то задача матиме множину розв'язків.
- n незалежних спостережень над випадковою величиною з законом розподілу F(z/a), що залежить від параметра a, значення якого невідомо. Довірчі межі випадкових похибок — це верхня та нижня межі інтервалу, в які похибки потрапляють із заданою ймовірністю Р. Величина Р називається довірчою ймовірністю. Для визначення довірчих меж похибок необхідно знати густину розподілу похибок та ймовірність потрапляння похибок у довірчі межі. Якщо не ввести обмеження, то задача матиме множину розв'язків.
- Визначення 1. Функція спостережень a1(x1,..., xn) (помітимо, що це випадкова величина) називається нижньою довірчою границею для параметра a з рівнем довіри РД (звичайно близьким до 1), якщо при будь-якому значенні виконується P
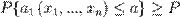 .
.
- Визначення 2. Функція спостережень a2(x1,..., xn) (випадкова величина) називається верхньою довірчою границею для параметра з рівнем довіри РД, якщо при будь-якім значенні
 .
.
- Визначення 3. Інтервал з випадковими кінцями (випадковий інтервал)
I(x) = (a1(x), a2(x)), обумовлений двома функціями спостережень, називається довірчим інтервалом для параметра a з рівнем довіри РД, якщо при будь-якім значенні a 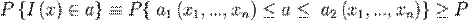 , тобто імовірність (що залежить від a) накрити випадковим інтервалом I(x) справжнє значення a - більше або дорівнює РД. Рівень довіри РД означає, що правило визначення інтервалу дає вірний результат з імовірністю РД, що звичайно вибирається близькою до 1, однак, 1 не дорівнює. Переконаємося статистично на прикладі в тім, що довірчий інтервал з рівнем довіри РД може не містити (з малою імовірністю 1- РД) істинне значення параметру.
, тобто імовірність (що залежить від a) накрити випадковим інтервалом I(x) справжнє значення a - більше або дорівнює РД. Рівень довіри РД означає, що правило визначення інтервалу дає вірний результат з імовірністю РД, що звичайно вибирається близькою до 1, однак, 1 не дорівнює. Переконаємося статистично на прикладі в тім, що довірчий інтервал з рівнем довіри РД може не містити (з малою імовірністю 1- РД) істинне значення параметру.