Классификация квадратичных форм. Необходимое и достаточное условие положительной (отрицательной) определенности квадратичных форм

Квадратичная форма называется положительно (отрицательно) определенной, если для всех значений выполняется условие (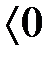), причем только при .

Теорема 4 Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все ее канонические коэффициенты положительны (отрицательны).

Угловым минором порядка () матрицы называется минор .

Теорема 5 (критерий Сильвестра положительной определенности квадратичной формы) Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все угловые миноры ее матрицы были положительны.

Матрица называется положительно определенной, если она является матрицей некоторой положительно определенной квадратичной формы (обозначение: ).

Говорят, что , если .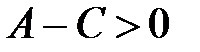

Теорема 6 (метод Якоби) Если (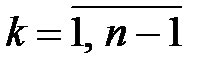), то существует единственное невырожденное линейное преобразование с треугольной матрицей, приводящее квадратичную форму к каноническому виду с каноническими коэффициентами , , .

Квадратичная форма называется неотрицательной (неположительной), если для всех значений выполняется условие 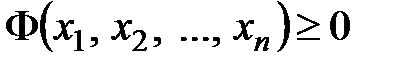().