Применение теории квадратичных форм к исследованию алгебраических уравнений второй степени

Рассмотренный выше метод ортогонального преобразования, приводящий квадратичную форму к каноническому виду, эффективно применяется при исследовании алгебраических уравнений второй степени с переменными:

, , (85)

где - квадратичная форма.

Рассмотрим некоторое евклидово пространство с ортонормированным базисом . Переменные в уравнении (85) будем интерпретировать как координаты элементов 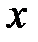некоторого множества из в ортонормированном базисе 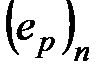. Пусть - множество элементов 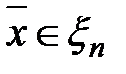, полученное из сдвигом на вектор – , т.е. , где 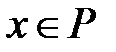, , - фиксированный элемент . Поэтому координаты элементов и в ортонормированном базисе связаны соотношениями , . Тогда уравнение (85) можно рассматривать как алгебраическое уравнение второй степени относительно координат элементов из . В 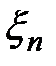всегда можно указать новый базис 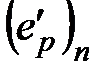, в котором квадратичная форма принимает канонический вид, и такое множество , что уравнение (85), рассматриваемое относительно координат элементов 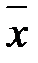в базисе , имеет наиболее простой вид. Чтобы сделать это, надо, во-первых, произвести ортогональное преобразование координат, приводящее квадратичную форму к каноническому виду, и, во-вторых, в преобразованном уравнении освободиться от линейных членов, выделяя полные квадраты.

Вопросы для самоконтроля

1. Какое пространство называется евклидовым пространством?

2. Какой базис в линейном пространстве называется ортонормированным?

3. Сформулируйте определение линейного оператора.

4. Какой оператор называется тождественным оператором?

5. Сформулируйте определение линейного оператора А.

6. Сформулируйте определение характеристического многочлена и характеристического уравнения линейного оператора А.

7. Какая матрица линейного оператора задает сдвиг двумерного и трехмерного пространства?

8. Сформулируйте определение квадратичной формы поверхности или линии второго порядка.

9. Запишите матрицу квадратичной формы .

10. Запишите матрицу поворота системы координат на плоскости.

11. Сформулируйте определение нормы вектора.

12. Сформулируйте определение ортогональных векторов.

13. Какая матрица линейного оператора задает растяжение (сжатие) двумерного и трехмерного пространства?

14. Какая матрица линейного оператора задает зеркальное отражение?

15. Найти собственные значения линейного оператора, заданного матрицей

16. Найти норму вектора 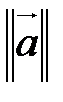, заданного в базисе

17. Сформулируйте критерий Сильвестра.

18. Метод Лагранжа.

19. Сформулируйте определение положительной (отрицательной) квадратичной формы.

20. Запишите формулы перехода от старого базиса к новому базису и наоборот.