А. Статистическая составляющая анализа качества модели

Анализ качества эконометрической модели

Эконометрический анализ зависимостей обычно начинается с оценки линейной зависимости переменных.

Но оценка параметров конкретного уравнения является лишь отдельным этапом длительного и сложного процесса построения эконометрической модели. Первое же оцененное уравнение очень редко является удовлетворительным во всех отношениях. Обычно приходится постепенно подбирать формулу связи и состав объясняющих переменных, анализируя на каждом этапе качество оцененной зависимости.

Анализ качества модели включает статистическую и содержательную составляющую.

А. Статистическая составляющая анализа качества модели

Проверка статистического качества оцененного уравнения состоит из следующих этапов.

Этап 1. Проверка общего качества уравнения регрессии

Для анализа общего качества оцененной регрессии обычно используют коэффициент детерминации 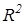. Он характеризует долю вариации (долю разброса) зависимой переменной, объясненной с помощью данного уравнения.

Для определения статистической значимости коэффициента детерминации проверяется нулевая гипотеза для F-статистики.

Этап 2. Проверка статистической значимости оценок параметров уравнения регрессии

Для проверки на статистическую значимость оценок параметров регрессии, определенных методом наименьших квадратов, используется распределение Стьюдента (Т-тест Стьюдента).

Этап 3. Проверка условий и свойств данных, выполнение которых предполагалось при оценивании уравнения регрессии

Близкое к единице значение коэффициента детерминации еще не свидетельство высокого качества уравнения регрессии.

Из уравнения модели 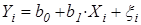видно, что 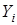зависит от объясняющей переменной 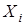и ошибки . Поэтому предпосылки (предположения) относительно переменной 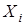и величины являются главными для интерпретации регрессионных оценок.

Для того чтобы оценки параметров, полученные с помощью МНК, обладали желательными свойствами (т.е. являлись несмещенными, состоятельными и эффективными), сделаем следующие предположения относительно свойств объясняющей переменной 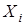и ошибок регрессионной модели:

1. Ошибки являются случайными величинами.

2. Математическое ожидание случайных величин равно нулю для всех i.

Предположение 2 утверждает, что факторы, неучтенные в модели и потому отнесенные к , не влияют систематически на математическое ожидание 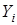. Т.е. положительные значения нейтрализуют отрицательные , поэтому их усредненное влияние на 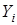равняется нулю (рис.3.4).

Из этого следует, что математическое ожидание 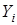, обусловленное 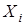, равно:

.

Рис.3.4. Графическая интерпретация предположения 2

3. Дисперсия случайных величин одинакова для всех i.

Предположение 3 означает гомоскедастичность (одинаковую дисперсию) всех случайных величин независимо от номера наблюдения i.

Т.е. дисперсия для каждого является постоянной (константой), равной . Из этого следует, что дисперсия распределения 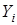также является постоянной величиной.

Ситуация, когда условие гомоскедастичности не выполняется, определяется как гетероскедастичность, или неодинаковая дисперсия.

Если предположение 3 нарушается (дисперсия распределения случайных величин не является постоянной), сразу возникает вопрос: какие распределения зависимой переменной Y выбирать для описания реальной ситуации – те, которые сосредоточены вокруг своих математических ожиданий или те, которые имеют большой разброс? Вводя предположение 3 (о гомоскедастичности) ограничиваются случаем, когда все значения Y, относящиеся к разным значениям Х, являются одинаково важными.

4. Значения случайных величин статистически независимы между собой.

Это гипотеза о некоррелированности ошибок для разных наблюдений.

Предположение 4 утверждает, что любое i -тое значение случайной величины не влияет на любое j -тое значение (i¹ j), иначе говоря, корреляция между и (i¹ j) отсутствует.

В случае, когда это условие не выполняется, говорят об автокорреляции остатков регрессии, а полученная формула регрессии считается обычно неудовлетворительной.

Это условие часто нарушается, когда наши данные являются временными рядами.

Предположение 4 дает возможность изучать систематическое влияние (если оно есть) Х на Y без учета влияния других факторов, выраженных случайной величиной . Если это не так, то мы будем иметь более сложную зависимость.

Проиллюстрируем на простом примере, что происходит в случае нарушения предположения 4. Предположим, что в регрессионной модели 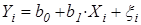случайные величины и 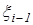имеют положительную корреляцию. Тогда 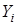будет зависеть не только от 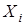, но и от 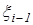, поскольку значение 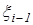некоторым образом определяет величину .

Статистическая независимость ошибок между собой является одним из основных предполагаемых свойств ошибок. При этом проверяется обычно их некоррелированность (являющаяся необходимым, но недостаточным атрибутом независимости), причем некоррелированность не любых, а соседних величин.

Некоррелированность отклонений от линии регрессии позволяет проверить DW-статистика (статистика Дарбина-Уотсона).

5. Значения случайной величины и значения переменной 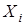независимы между собой.

Это условие предполагает отсутствие корреляции между случайной величиной и объясняющей переменной Х. В противном случае Х изменяется с изменением и сложно проследить влияние Х на Y.