Регрессионная модель специфицирована правильно.

Как отмечалось ранее, эконометрическое исследование начинается со спецификации модели, которая должна быть адекватной изучаемому экономическому процессу. Ранее также отмечалось, что спецификация модели – это наше представление о механизме зависимости переменных (например, 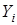от 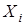) и сам выбор объясняющей переменной Х. Теперь уточним вопросы, решаемые при спецификации модели.

При спецификации модели возникает несколько важных вопросов, а именно:

- какие переменные необходимо включать в модель;

- какова функциональная форма связи переменных модели;

- является ли модель линейной по параметрам и по переменным, или нет;

- какие возможные предположения относительно 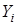, 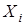и можно сделать в модели?

Это чрезвычайно важные вопросы, т.к., например, исключая из модели важные переменные, или выбирая неправильную функциональную форму связи, или делая неправильные предположения относительно переменных модели, мы ставим под сомнение правильность интерпретации оцененной регрессии.

Чтобы дать представление о важности предположения 6, представим, что для массива наблюдений, изображенного на рис.3.5, мы можем выбрать две разные модели, отражающие связь между Y и X:

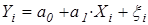; (3.11)

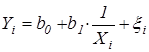. (3.12)

Регрессионная модель (3.11) является линейной и по параметрам и по переменным, в то время как модель (3.12) является линейной по параметрам (т.е. моделью линейной регрессии по нашему определению), но нелинейной по переменной Х.

Рис.3.5. Линейная и нелинейная модели

Если в действительности «правильной» является модель (3.12), а мы выбрали модель (3.11), то, как показано на рис.3.5, модель (3.11) даст неправильное представление об Y по значениям Х: между точками А и В для любого модель (3.11) будет переоценивать действительное математическое ожидание Y, и в тоже время будет недооценивать математическое ожидание Y слева от А и справа от В).

Этот условный пример является образцом того, что называется неправильной спецификацией, или ошибкой спецификации, которая заключается в выборе неправильной функциональной формы связи: на рис.3.5 реальная взаимосвязь величин Х и Y описывается нелинейной функцией (2), и какую бы мы ни провели прямую линию (например, 1), отклонения точек наблюдений от нее будут существенными и неслучайными.

7. Случайные величины распределены нормально с нулевым математическим ожиданием и постоянной дисперсией .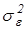

Свойства оценок (несмещенность, состоятельность и эффективность) не зависят от конкретного вида распределения величин . Тем не менее, обычно предполагается, что они распределены нормально. Эта предпосылка необходима:

- для проверки статистической значимости сделанных оценок;

- для построения доверительных интервалов для параметров и для зависимой переменной Y.

Дело в том, что t-статистики распределены по закону Стьюдента, если выборка взята из генеральной совокупности с нормальным распределением ошибок.

Выводы.

Итак, приступая к оценке линейного уравнения регрессии с двумя переменными, мы предполагаем, что реальная взаимосвязь переменных линейна, а отклонения от регрессионной прямой случайны, независимы между собой и имеют нулевое среднее значение и постоянную дисперсию. Если это не так, то наш анализ статистической значимости МНК-оценок параметров регрессии неточен, а сами МНК-оценки этих параметров не обладают такими желательными свойствами, как несмещенность, состоятельность и эффективность.

Попытаемся ответить на вопрос, в каких случаях остатки регрессии (остатки регрессии – это наблюдаемые значения ошибок ) не обладают предполагавшимися свойствами.

Мы видим, например, на рис.3.5, что в этом случае отклонения от линии регрессии (1) не случайно распределены вокруг нее, а обладают определенной закономерностью. Эта закономерность, в частности, выражается в одинаковом, как правило, знаке каждых двух соседних отклонений. Это может являться:

1) следствием нелинейного характера связи переменных;

2) воздействием какого-то фактора, не включенного в уравнение регрессии. Величина такого неучтенного фактора может менять свою динамику в рассматриваемый период, отклоняясь в достаточно длительные промежутки времени в ту или иную сторону от своего среднего значения. Это, очевидно, может служить причиной длительных устойчивых отклонений зависимой переменной от линии регрессии.

Обе указанные причины свидетельствуют о том, что существует возможность улучшить уравнение регрессии путем оценивания какой-то новой нелинейной формулы или включения некоторой новой объясняющей переменной.